Cone (formal languages)
In formal language theory, a cone is a set of formal languages that has some desirable closure properties enjoyed by some well-known sets of languages, in particular by the families of regular languages, context-free languages and the recursively enumerable languages.[1] The concept of a cone is a more abstract notion that subsumes all of these families. A similar notion is the faithful cone, having somewhat relaxed conditions. For example, the context-sensitive languages do not form a cone, but still have the required properties to form a faithful cone.
The terminology cone has a French origin. In the American oriented literature one usually speaks of a full trio. The trio corresponds to the faithful cone.
Definition
A cone is a non-empty family 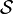 of languages such that, for any
of languages such that, for any 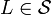 over some alphabet
over some alphabet 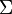 ,
,
- if
 is a homomorphism from
is a homomorphism from 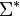 to some
to some 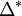 , the language
, the language 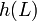 is in
is in 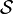 ;
; - if
 is a homomorphism from some
is a homomorphism from some 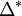 to
to 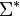 , the language
, the language 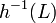 is in
is in 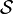 ;
; - if
 is any regular language over
is any regular language over 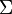 , then
, then 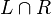 is in
is in 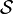 .
.
The family of all regular languages is contained in any cone.
If one restricts the definition to homomorphisms that do not introduce the empty word  then one speaks of a faithful cone; the inverse homomorphisms are not restricted. Within the Chomsky hierarchy, the regular languages, the context-free languages, and the recursively enumerable languages are all cones, whereas the context-sensitive languages and the recursive languages are only faithful cones.
then one speaks of a faithful cone; the inverse homomorphisms are not restricted. Within the Chomsky hierarchy, the regular languages, the context-free languages, and the recursively enumerable languages are all cones, whereas the context-sensitive languages and the recursive languages are only faithful cones.
Relation to Transducers
A finite state transducer is a finite state automaton that has both input and output. It defines a transduction  , mapping a language
, mapping a language  over the input alphabet into another language
over the input alphabet into another language 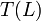 over the output alphabet. Each of the cone operations (homomorphism, inverse homomorphism, intersection with a regular language) can be implemented using a finite state transducer. And, since finite state transducers are closed under composition, every sequence of cone operations can be performed by a finite state transducer.
over the output alphabet. Each of the cone operations (homomorphism, inverse homomorphism, intersection with a regular language) can be implemented using a finite state transducer. And, since finite state transducers are closed under composition, every sequence of cone operations can be performed by a finite state transducer.
Conversely, every finite state transduction  can be decomposed into cone operations. In fact, there exists a normal form for this decomposition,[2] which is commonly known as Nivat's Theorem:[3]
Namely, each such
can be decomposed into cone operations. In fact, there exists a normal form for this decomposition,[2] which is commonly known as Nivat's Theorem:[3]
Namely, each such  can be effectively decomposed as
can be effectively decomposed as
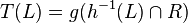 , where
, where 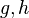 are homomorphisms, and
are homomorphisms, and  is a regular language depending only on
is a regular language depending only on  .
.
Altogether, this means that a family of languages is a cone if it is closed under finite state transductions. This is a very powerful set of operations. For instance one easily writes a (nondeterministic) finite state transducer with alphabet 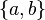 that removes every second
that removes every second  in words of even length (and does not change words otherwise). Since the context-free languages form a cone, they are closed under this exotic operation.
in words of even length (and does not change words otherwise). Since the context-free languages form a cone, they are closed under this exotic operation.
See also
Notes
References
- Ginsburg, Seymour; Greibach, Sheila (1967). "Abstract Families of Languages". Conference Record of 1967 Eighth Annual Symposium on Switching and Automata Theory, 18–20 October 1967, Austin, Texas, USA. IEEE. pp. 128–139.
- Nivat, Maurice (1968). "Transductions des langages de Chomsky". Annales de l'institut Fourier 18 (1): 339–455. doi:10.5802/aif.287.
- Seymour Ginsburg, Algebraic and automata theoretic properties of formal languages, North-Holland, 1975, ISBN 0-7204-2506-9.
- John E. Hopcroft and Jeffrey D. Ullman, Introduction to Automata Theory, Languages, and Computation, Addison-Wesley Publishing, Reading Massachusetts, 1979. ISBN 0-201-02988-X. Chapter 11: Closure properties of families of languages.
- Mateescu, Alexandru; Salomaa, Arto (1997). "Chapter 4: Aspects of Classical Language Theory". In Rozenberg, Grzegorz; Salomaa, Arto. Handbook of Formal Languages. Volume I: Word, language, grammar. Springer-Verlag. pp. 175–252. ISBN 3-540-61486-9.
External links
- Encyclopedia of mathematics: Trio, Springer.