Conditional expectation
In probability theory, the conditional expectation of a random variable is another random variable equal to the average of the former over each possible "condition". In the case when the random variable is defined over a discrete probability space, the "conditions" are a partition of this probability space. This definition is then generalized to any probability space using measure theory.
Conditional expectation is also known as conditional expected value or conditional mean.
In modern probability theory the concept of conditional probability is defined in terms of conditional expectation.
Concept
The concept of conditional expectation can be nicely illustrated through the following example. Suppose we have daily rainfall data (mm of rain each day) collected by a weather station on every day of the ten year period from Jan 1, 1990 to Dec 31, 1999. The conditional expectation of daily rainfall knowing the month of the year is the average of daily rainfall over all days of the ten year period that fall in a given month. These data then may be considered either as a function of each day (so for example its value for Mar 3, 1992, would be the sum of daily rainfalls on all days that are in the month of March during the ten years, divided by the number of these days, which is 310) or as a function of just the month (so for example the value for March would be equal to the value of the previous example).
It is important to note the following.
- The conditional expectation of daily rainfall knowing that we are in a month of March of the given ten years is not a monthly rainfall data, that is it is not the average of the ten monthly total March rainfalls. That number would be 31 times higher.
- The average daily rainfall in March 1992 is not equal to the conditional expectation of daily rainfall knowing that we are in a month of March of the given ten years, because we have restricted ourselves to 1992, that is we have more conditions than just that of being in March. This shows that reasoning as "we are in March 1992, so I know we are in March, so the average daily rainfall is the March average daily rainfall" is incorrect. Stated differently, although we use the expression "conditional expectation knowing that we are in March" this really means "conditional expectation knowing nothing other than that we are in March".
History
The related concept of conditional probability dates back at least to Laplace who calculated conditional distributions. It was Andrey Kolmogorov who in 1933 formalized it using the Radon–Nikodym theorem.[1] In works of Paul Halmos[2] and Joseph L. Doob[3] from 1953, conditional expectation was generalized to its modern definition using sub-sigma-algebras.[4]
Classical definition
Conditional expectation with respect to an event
In classical probability theory the conditional expectation of X given an event H (which may be the event Y=y for a random variable Y) is the average of X over all outcomes in H, that is
The sum above can be grouped by different values of 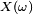 , to get a sum over the range
, to get a sum over the range  of X
of X
In modern probability theory, when H is an event with strictly positive probability, it is possible to give a similar formula. This is notably the case for a discrete random variable Y and for y in the range of Y if the event H is Y=y. Let  be a probability space, X a random variable on that probability space, and
be a probability space, X a random variable on that probability space, and 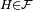 an event with strictly positive probability
an event with strictly positive probability 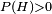 . Then the conditional expectation of X given the event H is
. Then the conditional expectation of X given the event H is
where  is the range of X and
is the range of X and  is the conditional probability of A knowing H.
is the conditional probability of A knowing H.
When P(H) = 0 (for instance if Y is a continuous random variable and H is the event Y=y, this is in general the case), the Borel–Kolmogorov paradox demonstrates the ambiguity of attempting to define the conditional probability knowing the event H. The above formula shows that this problem transposes to the conditional expectation. So instead one only defines the conditional expectation with respect to a sigma-algebra or a random variable.
Conditional expectation with respect to a random variable
If Y is a discrete random variable with range  , then we can define on
, then we can define on  the function
the function
Sometimes this function is called the conditional expectation of X with respect to Y. In fact, according to the modern definition, it is  that is called the conditional expectation of X with respect to Y, so that we have
that is called the conditional expectation of X with respect to Y, so that we have
which is a random variable.
As mentioned above, if Y is a continuous random variable, it is not possible to define  by this method. As explained in the Borel–Kolmogorov paradox, we have to specify what limiting procedure produces the set Y = y. This can be naturally done by defining the set
by this method. As explained in the Borel–Kolmogorov paradox, we have to specify what limiting procedure produces the set Y = y. This can be naturally done by defining the set 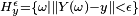 , and taking the limit
, and taking the limit 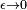 , so that if
, so that if  for all
for all  , then
, then
-
 .
.
The modern definition is analogous to the above except that the above limiting process is replaced by the Radon–Nikodym derivative, so the result holds more generally.
Formal definition
Conditional expectation with respect to a σ-algebra

 is the [0,1] interval with the Lebesgue measure. We define the following σ-algebras:
is the [0,1] interval with the Lebesgue measure. We define the following σ-algebras: 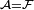 while
while  is the σ-algebra generated by the intervals with end-points 0, ¼, ½, ¾, 1 and
is the σ-algebra generated by the intervals with end-points 0, ¼, ½, ¾, 1 and  is the σ-algebra generated by the intervals with end-points 0, ½, 1. Here the conditional expectation is effectively the average over the minimal sets of the σ-algebra.
is the σ-algebra generated by the intervals with end-points 0, ½, 1. Here the conditional expectation is effectively the average over the minimal sets of the σ-algebra.Consider the following
-
 is a probability space
is a probability space -
 is a random variable on that probability space
is a random variable on that probability space -
 is a sub-σ-algebra of
is a sub-σ-algebra of 
Then a conditional expectation of X given  , denoted as
, denoted as 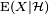 , is any
, is any  -measurable function
(
-measurable function
( ) which satisfies:
) which satisfies:
 .[5]
.[5]
The existence of 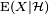 can be established by noting that
can be established by noting that 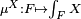 for
for  is a measure on
is a measure on  that is absolutely continuous with respect to
that is absolutely continuous with respect to  . Furthermore, if
. Furthermore, if  is the natural injection from
is the natural injection from  to
to  then
then  is the restriction of
is the restriction of  to
to  and
and  is the restriction of
is the restriction of  to
to  and
and 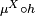 is absolutely continuous with respect to
is absolutely continuous with respect to 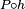 since
since  . Thus, we have
. Thus, we have
where the derivatives are Radon–Nikodym derivatives of measures.
Conditional expectation with respect to a random variable
Consider further to the above
-
 is a measurable space
is a measurable space -
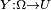 is a random variable
is a random variable
Then for any  -measurable function
-measurable function  which satisfies:
which satisfies:
 .
.
the random variable  , denoted as
, denoted as  , is a conditional expectation of X given
, is a conditional expectation of X given  .
.
This definition is equivalent to defining the conditional expectation using the pre-image of Σ with respect to Y. If we define
then
 .
.
Discussion
A couple of points worth noting about the definition:
- This is not a constructive definition; we are merely given the required property that a conditional expectation must satisfy.
- The definition of
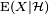 may resemble that of
may resemble that of  for an event
for an event  but these are very different objects, the former being a
but these are very different objects, the former being a  -measurable function
-measurable function  , while the latter is an element of
, while the latter is an element of  for fixed
for fixed  , or a function
, or a function  if considered as the function
if considered as the function  .
. - Existence of a conditional expectation function is determined by the Radon–Nikodym theorem, a sufficient condition is that the (unconditional) expected value for X exist.
- Uniqueness can be shown to be almost sure: that is, versions of the same conditional expectation will only differ on a set of probability zero.
- The definition of
- The σ-algebra
 controls the "granularity" of the conditioning. A conditional expectation
controls the "granularity" of the conditioning. A conditional expectation  over a finer-grained σ-algebra
over a finer-grained σ-algebra  will allow us to condition on a wider variety of events.
will allow us to condition on a wider variety of events.
Conditioning as factorization
In the definition of conditional expectation that we provided above, the fact that 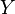 is a real random element is irrelevant. Let
is a real random element is irrelevant. Let  be a measurable space, where
be a measurable space, where 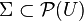 is a σ-algebra in
is a σ-algebra in 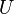 . A
. A 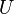 -valued random element is a measurable function
-valued random element is a measurable function  , i.e.
, i.e.  for all
for all  . The distribution of
. The distribution of 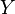 is the probability measure
is the probability measure  such that
such that  .
.
Theorem. If  is an integrable random variable, then there exists a
is an integrable random variable, then there exists a 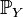 -unique integrable random element
-unique integrable random element  , such that
, such that
for all  .
.
Proof sketch
Let  be such that
be such that  . Then
. Then  is a signed measure which is absolutely continuous with respect to
is a signed measure which is absolutely continuous with respect to 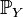 . Indeed
. Indeed  means exactly that
means exactly that  . Since the integral of an integrable function on a set of probability 0 is 0, this proves absolute continuity. The Radon–Nikodym theorem then proves the existence of a density of
. Since the integral of an integrable function on a set of probability 0 is 0, this proves absolute continuity. The Radon–Nikodym theorem then proves the existence of a density of  with respect to
with respect to 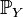 , which we denote by
, which we denote by 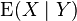 .
. 
Comparing with conditional expectation with respect to sub-sigma algebras, it holds that
We can further interpret this equality by considering the abstract change of variables formula to transport the integral on the right hand side to an integral over Ω:
The equation means that the integrals of  and the composition
and the composition  over sets of the form
over sets of the form 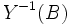 , for
, for  , are identical.
, are identical.
This equation can be interpreted to say that the following diagram is commutative in the average.
Computation
When X and Y are both discrete random variables, then the conditional expectation of X given the event Y=y can be considered as function of y for y in the range of Y
where  is the range of X.
is the range of X.
If X is a continuous random variable, while Y remains a discrete variable, the conditional expectation is:
with  (where fX,Y(x, y) gives the joint density of X and Y) is the conditional density of X given Y=y.
(where fX,Y(x, y) gives the joint density of X and Y) is the conditional density of X given Y=y.
If both X and Y are continuous random variables, then the conditional expectation is:
where  (where fY(y) gives the density of Y).
(where fY(y) gives the density of Y).
Basic properties
All the following formulas are to be understood in an almost sure sense.
The sigma-algebra  could be replaced by a random variable
could be replaced by a random variable 
- Pulling out independent factors:
- If
 is independent of
is independent of  , then
, then 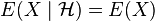 .
.
- If
Let 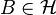 . Then
. Then  is independent of
is independent of  , so we get that
, so we get that
Thus the definition of conditional expectation is satisfied by the constant random variable  , as desired.
, as desired.
- If
 is independent of
is independent of  , then
, then  . Note that this is not necessarily the case if
. Note that this is not necessarily the case if  is only independent of
is only independent of  and of
and of 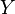 .
. - If
 are independent,
are independent,  are independent,
are independent,  is independent of
is independent of  and
and 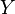 is independent of
is independent of  , then
, then 
- If
- Stability:
- If
 is
is  -measurable, then
-measurable, then  .
. - If Z is a random variable, then
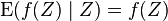 and in its simplest form:
and in its simplest form: 
- If
- Pulling out known factors:
- If
 is
is  -measurable, then
-measurable, then  .
. - If Z is a random variable, then

- If
- Tower property: for sub-σ-algebras
 we have
we have 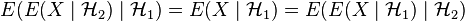 .
.
- A special case is when Z is a
 -measurable random variable. Then
-measurable random variable. Then 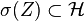 and thus
and thus 
- Doob martingale property: the above with
 (which is
(which is  -measurable), and using also
-measurable), and using also  , gives
, gives  .
.
- A special case is when Z is a
- Linearity: we have
 and
and  for
for 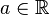 .
.
- Positivity: If
 then
then 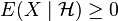 .
.
- Monotonicity: If
 then
then  .
.
- Monotone convergence: If
 then
then 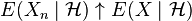 .
.
- Dominated convergence: If
 and
and  with
with  then
then 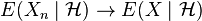 .
.
- Fatou's lemma: If
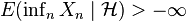 then
then  .
.
- Jensen's inequality: If
 is a convex function, then
is a convex function, then  .
.
- Conditional variance: Using the conditional expectation we can define, by analogy with the definition of the variance as the mean square deviation from the average, the conditional variance
- Definition:
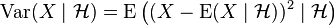
- Algebraic formula for the variance:

- Law of total variance:
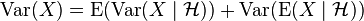 .
.
- Definition:
- Martingale convergence: For a random variable
 , that has finite expectation, we have
, that has finite expectation, we have 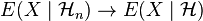 , if either
, if either  is an increasing series of sub-σ-algebras and
is an increasing series of sub-σ-algebras and  or if
or if  is a decreasing series of sub-σ-algebras and
is a decreasing series of sub-σ-algebras and  .
.
- Conditional expectation as
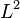 -projection: If
-projection: If  are in the Hilbert space of square-integrable real random variables (real random variables with finite second moment) then
are in the Hilbert space of square-integrable real random variables (real random variables with finite second moment) then
- for
 -measurable
-measurable 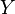 we have
we have 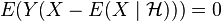 , i.e. the conditional expectation
, i.e. the conditional expectation  is in the sense of the L2(P) scalar product the orthogonal projection from
is in the sense of the L2(P) scalar product the orthogonal projection from  to the linear subspace of
to the linear subspace of  -measurable functions. (This allows to define and prove the existence of the conditional expectation based on the Hilbert projection theorem.)
-measurable functions. (This allows to define and prove the existence of the conditional expectation based on the Hilbert projection theorem.) - the mapping
 is self-adjoint:
is self-adjoint: 
- for
- Conditioning is a contractive projection of Lp spaces
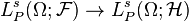 i.e.
i.e. 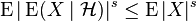 for any s ≥ 1.
for any s ≥ 1.
See also
- Non-commutative conditional expectation
- Law of total probability
- Law of total expectation
- Law of total variance
- Law of total cumulance (generalizes the other three)
- Conditioning (probability)
- Joint probability distribution
- Disintegration theorem
Notes
- ↑ Kolmogorov, Andrey (1933). Grundbegriffe der Wahrscheinlichkeitsrechnung (in German). Berlin: Julius Springer. p. 46.
- Translation: Kolmogorov, Andrey (1956). Foundations of the Theory of Probability (2nd ed.). New York: Chelsea. ISBN 0-8284-0023-7.
- ↑ Oxtoby, J. C. (1953). "Review: Measure theory, by P. R. Halmos" (PDF). Bull. Amer. Math. Soc. 59 (1): 89–91. doi:10.1090/s0002-9904-1953-09662-8.
- ↑ J. L. Doob (1953). Stochastic Processes. John Wiley & Sons. ISBN 0-471-52369-0.
- ↑ Olav Kallenberg: Foundations of Modern Probability. 2. edition. Springer, New York 2002, ISBN 0-387-95313-2, S. 573.
- ↑ Billingsley, Patrick (1995). "Section 34. Conditional Expectation". Probability and Measure (3rd ed.). John Wiley & Sons. p. 445. ISBN 0-471-00710-2.
References
- William Feller, An Introduction to Probability Theory and its Applications, vol 1, 1950, page 223
- Paul A. Meyer, Probability and Potentials, Blaisdell Publishing Co., 1966
- Grimmett, Geoffrey; Stirzaker, David (2001). Probability and Random Processes (3rd ed.). Oxford University Press. ISBN 0-19-857222-0., pages 67–69
External links
- Ushakov, N.G. (2001), "Conditional mathematical expectation", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4


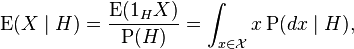



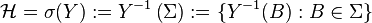


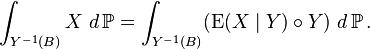
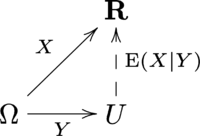




 .
.