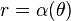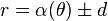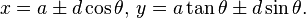Conchoid (mathematics)
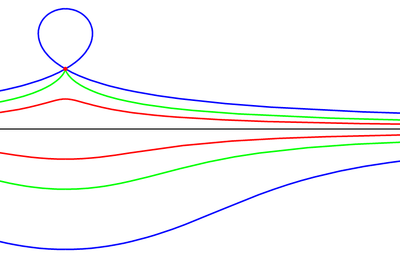
The fixed point O is the red dot, the black line is the given curve, and each pair of coloured curves is length d from the intersection with the line that a ray through O makes. In the blue case d is greater than O's distance from the line, so the upper blue curve loops back on itself. In the green case d is the same, and in the red case it's less.
A conchoid is a curve derived from a fixed point O, another curve, and a length d.
Description
For every line through O that intersects the given curve at A the two points on the line which are d from A are on the conchoid. The conchoid is, therefore, the cissoid of the given curve and a circle of radius d and center O. They are called conchoids because the shape of their outer branches resembles conch shells.
The simplest expression uses polar coordinates with O at the origin. If
expresses the given curve, then
expresses the conchoid.
If the curve is a line, then the conchoid is the conchoid of Nicomedes.
For instance, if the curve is the line  , then the line's polar form is
, then the line's polar form is
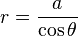 and therefore the conchoid can be expressed parametrically as
and therefore the conchoid can be expressed parametrically as
A limaçon is a conchoid with a circle as the given curve.
The so-called conchoid of de Sluze and conchoid of Dürer are not actually conchoids. The former is a strict cissoid and the latter a construction more general yet.
See also
References
- J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 36, 49–51, 113, 137. ISBN 0-486-60288-5.
- "Conchoïde" at Encyclopédie des Formes Mathématiques Remarquables
External links
![]() Media related to Conchoid at Wikimedia Commons
Media related to Conchoid at Wikimedia Commons