Concave polygon
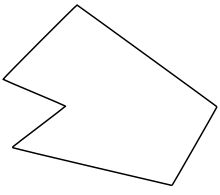
An example of a concave polygon.
A simple polygon that is not convex is called concave,[1] non-convex[2] or reentrant.[3] A simple concave polygon will always have an interior angle with a measure that is greater than 180 degrees.[4]
It is always possible to partition a concave polygon into a set of convex polygons. A polynomial-time algorithm for finding a decomposition into as few convex polygons as possible is described by Chazelle & Dobkin (1985).[5]
Notes
- ↑ McConnell, Jeffrey J. (2006), Computer Graphics: Theory Into Practice, p. 130, ISBN 0-7637-2250-2.
- ↑ Leff, Lawrence (2008), Let's Review: Geometry, Hauppauge, NY: Barron's Educational Series, p. 66, ISBN 978-0-7641-4069-3
- ↑ Mason, J.I. (1946), "On the angles of a polygon", The Mathematical Gazette (The Mathematical Association) 30 (291): 237–238, JSTOR 3611229.
- ↑ Definition and properties of concave polygons with interactive animation.
- ↑ Chazelle, Bernard; Dobkin, David P. (1985), "Optimal convex decompositions", in Toussaint, G.T., Computational Geometry (PDF), Elsevier, pp. 63–133.
External links
This article is issued from Wikipedia - version of the Tuesday, May 05, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.