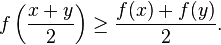Concave function
In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.
Definition
A real-valued function f on an interval (or, more generally, a convex set in vector space) is said to be concave if, for any x and y in the interval and for any t in [0,1],
A function is called strictly concave if
for any t in (0,1) and x ≠ y.
For a function f:R→R, this definition merely states that for every z between x and y, the point (z, f(z) ) on the graph of f is above the straight line joining the points (x, f(x) ) and (y, f(y) ).

A function f is quasiconcave if the upper contour sets of the function 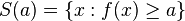 are convex sets.[1]:496
are convex sets.[1]:496
Properties
A function f is concave over a convex set if and only if the function −f is a convex function over the set.
A differentiable function f is concave on an interval if its derivative function f ′ is monotonically decreasing on that interval: a concave function has a decreasing slope. ("Decreasing" here means non-increasing, rather than strictly decreasing, and thus allows zero slopes.)
Points where concavity changes (between concave and convex) are inflection points.
Near a local maximum in the interior of the domain of a function, the function must be concave; as a partial converse, if the derivative of a strictly concave function is zero at some point, then that point is a local maximum.
If f is twice-differentiable, then f is concave if and only if f ′′ is non-positive (or, if the acceleration is non-positive). If its second derivative is negative then it is strictly concave, but the opposite is not true, as shown by f(x) = −x4.
If f is concave and differentiable, then it is bounded above by its first-order Taylor approximation:[1]:489
A continuous function on C is concave if and only if for any x and y in C
If a function f is concave, and f(0) ≥ 0, then f is subadditive. Proof:
- since f is concave, let y = 0,
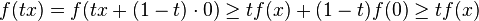
-
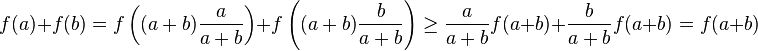
Examples
- The functions
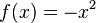 and
and 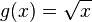 are concave on their domains, as their second derivatives
are concave on their domains, as their second derivatives 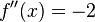 and
and 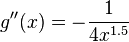 are always negative.
are always negative. - The logarithm function
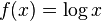 is concave on its domain
is concave on its domain 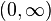 , as its derivative
, as its derivative  is a strictly decreasing function.
is a strictly decreasing function. - Any affine function
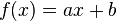 is both (non-strictly) concave and convex.
is both (non-strictly) concave and convex. - The sine function is concave on the interval
![[0, \pi]](../I/m/e1868564b62b4e2f1c063321df289469.png) .
. - The function
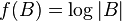 , where
, where 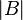 is the determinant of a nonnegative-definite matrix B, is concave.[2]
is the determinant of a nonnegative-definite matrix B, is concave.[2] - Practical example: rays bending in computation of radiowave attenuation in the atmosphere.
See also
- Concave polygon
- Convex function
- Jensen's inequality
- Logarithmically concave function
- Quasiconcave function
References
- 1 2 Varian, Hal (1992). Microeconomic Analysis (Third ed.). New York: Norton. ISBN 0393957357.
- ↑ Thomas M. Cover and J. A. Thomas (1988). "Determinant inequalities via information theory". SIAM Journal on Matrix Analysis and Applications 9 (3): 384–392. doi:10.1137/0609033.
- Crouzeix, J.-P. (2008). "Quasi-concavity". In Durlauf, Steven N.; Blume, Lawrence E. The New Palgrave Dictionary of Economics (Second ed.). Palgrave Macmillan. doi:10.1057/9780230226203.1375.
- Rao, Singiresu S. (2009). Engineering Optimization: Theory and Practice. John Wiley and Sons. p. 779. ISBN 0-470-18352-7.
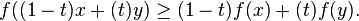
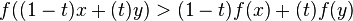
![f(y) \leq f(x) + f'(x)[y-x].](../I/m/5714bd090bbe381e3d0087e23bc0cc94.png)