Recursive ordinal

In mathematics, specifically set theory, an ordinal $\alpha$ is said to be recursive if there is a recursive well-ordering of a subset of the natural numbers having the order type $\alpha$ .

It is trivial to check that 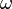$\omega$ is recursive, the successor of a recursive ordinal is recursive, and the set of all recursive ordinals is closed downwards. The supremum of all recursive ordinals is called the Church-Kleene ordinal and denoted by 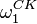$\omega^{CK}_1$ . Indeed, an ordinal is recursive if and only if it is smaller than 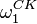$\omega^{CK}_1$ . Since there are only countably many recursive relations, there are also only countably many recursive ordinals. Thus, 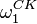$\omega^{CK}_1$ is countable.

The recursive ordinals are exactly the ordinals that have an ordinal notation in Kleene's $\mathcal{O}$ .

References

Rogers, H. The Theory of Recursive Functions and Effective Computability, 1967. Reprinted 1987, MIT Press, ISBN 0-262-68052-1 (paperback), ISBN 0-07-053522-1
Sacks, G. Higher Recursion Theory. Perspectives in mathematical logic, Springer-Verlag, 1990. ISBN 0-387-19305-7

This article is issued from Wikipedia - version of the Tuesday, March 20, 2012. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Recursive ordinal

See also

References