Compound matrix

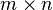In mathematics, the kth compound matrix (sometimes referred to as the kth multiplicative compound matrix) $C_k(A)$ ,^[1] of an $m\times n$ matrix A is the 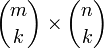$\binom m k\times \binom n k$ matrix formed from the determinants of all 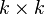$k\times k$ submatrices of A, i.e., all 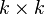$k\times k$ minors, arranged with the submatrix index sets in lexicographic order.

\begin{align} C_1(A) & = A \\[6pt] C_n(A) & = \det(A)\text{ if }A\text{ is }n\times n \\[6pt] C_k(AB) & = C_k(A)C_k(B) \\[6pt] C_k(aX) & = a^kC_k(X) \\[6pt] \text{For } n\times n \text{ identity } I, C_k(I) & = I\,, \text{ the }\textstyle{\binom n k\times \binom n k} \text{ identity }\\[6pt] C_k(A^T) & = C_k(A)^T\,, \text{ over any field} \\[6pt] C_k(A^*) & = C_k(A)^*\,, \text{ over } \mathbb{C} \\[6pt] C_k(A^{-1}) & = C_k(A)^{-1}\,, \text{ for } n\times n, \text{ invertible } A \end{align}

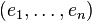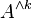If $A$ is viewed as the matrix of an operator in a basis $(e_1,\dots,e_n)$ then the compound matrix $C_k(A)$ is the matrix of the $k$ -th exterior power $A^{\wedge k}$ in the basis $(e_{i_1} \wedge \dots \wedge e_{i_k}, i_1 < \dots < i_k)$ . In this formulation, the multiplicativity property stated above is equivalent to the functoriality of the exterior power.

References

↑ R.A. Horn and C.R. Johnson, Matrix Analysis, Cambridge University Press, 1990, pp. 19–20

External links

Gantmacher, F. R. and Krein, M. G., Oscillation Matrices and Kernels and Small Vibrations of Mechanical Systems, Revised Edition, http://www.ams.org/bookstore?fn=20&arg1=diffequ&ikey=CHEL-345-H
To efficiently calculate compound matrices see: "Compound matrices: properties, numerical issues and analytical computations" - Christos Kravvaritis · Marilena Mitrouli - DOI 10.1007/s11075-008-9222-7

This article is issued from Wikipedia - version of the Thursday, December 24, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.