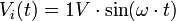Complex gain
In electronics, Complex gain is the effect circuitry has on the amplitude and phase of a sine wave signal. The term complex is used because mathematically this effect can be expressed as a complex number.
Example
Suppose a circuit has an input voltage described by the equation
where ω equals 2π×100Hz, i.e., the input signal is a 100Hz sine wave with an amplitude of 1 Volt.
If the circuit is such that for this frequency it doubles the signal's amplitude and causes a 90 degrees forward phase shift, then its output signal can be described by
In complex notation, these signals can be described as, for this frequency, j·1V and 2V, respectively.
The complex gain G of this circuit is then computed by dividing output by input:
This (unitless) complex number incorporates both the magnitude of the change in amplitude (as the absolute value) and the phase change (as the argument).