Complex convexity
Definition
A set  in
in  is called
is called 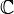 -convex if its intersection with any complex line is contractible.[1]
-convex if its intersection with any complex line is contractible.[1]
Background
In complex geometry and analysis, the notion of convexity and its generalizations play an important role in understanding function behavior. Examples of classes of functions with a rich structure are, in addition to the convex functions, the subharmonic functions and the plurisubharmonic functions. Geometrically, these classes of functions correspond to convex domains and pseudoconvex domains, but there are also other types of domains, for instance lineally convex domains which can be generalized using convex analysis. A great deal is already known about these domains, but there remain some fascinating, unsolved problems. This theme is mainly theoretical, but there are computational aspects of the domains studied, and these computational aspects are certainly worthy of further study.