Comparison triangle
Define 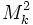 as the 2-dimensional metric space of constant curvature
as the 2-dimensional metric space of constant curvature  . So, for example,
. So, for example,  is the Euclidean plane,
is the Euclidean plane, 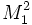 is the surface of the unit sphere, and
is the surface of the unit sphere, and  is the hyperbolic plane.
is the hyperbolic plane.
Let  be a metric space. Let
be a metric space. Let  be a triangle in
be a triangle in  , with vertices
, with vertices  ,
, 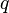 and
and  . A comparison triangle
. A comparison triangle  in
in 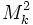 for
for  is a triangle in
is a triangle in 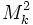 with vertices
with vertices 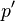 ,
,  and
and  such that
such that  ,
,  and
and 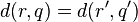 .
.
Such a triangle is unique up to isometry.
The interior angle of  at
at 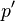 is called the comparison angle between
is called the comparison angle between 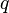 and
and  at
at  . This is well-defined provided
. This is well-defined provided 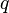 and
and  are both distinct from
are both distinct from  .
.
References
- M Bridson & A Haefliger - Metric Spaces Of Non-Positive Curvature, ISBN 3-540-64324-9
This article is issued from Wikipedia - version of the Thursday, February 17, 2011. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.