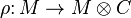Comodule
In mathematics, a comodule or corepresentation is a concept dual to a module. The definition of a comodule over a coalgebra is formed by dualizing the definition of a module over an associative algebra.
Formal definition
Let K be a field, and C be a coalgebra over K. A (right) comodule over C is a K-vector space M together with a linear map
such that
-
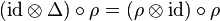
-
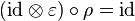 ,
,
where Δ is the comultiplication for C, and ε is the counit.
Note that in the second rule we have identified 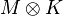 with
with 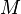 .
.
Examples
- A coalgebra is a comodule over itself.
- If M is a finite-dimensional module over a finite-dimensional K-algebra A, then the set of linear functions from A to K forms a coalgebra, and the set of linear functions from M to K forms a comodule over that coalgebra.
- A graded vector space V can be made into a comodule. Let I be the index set for the graded vector space, and let
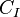 be the vector space with basis
be the vector space with basis  for
for  . We turn
. We turn 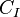 into a coalgebra and V into a
into a coalgebra and V into a 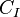 -comodule, as follows:
-comodule, as follows:
- Let the comultiplication on
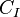 be given by
be given by 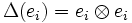 .
. - Let the counit on
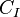 be given by
be given by 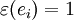 .
. - Let the map
 on V be given by
on V be given by 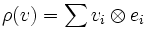 , where
, where  is the i-th homogeneous piece of
is the i-th homogeneous piece of 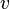 .
.
- Let the comultiplication on
Rational comodule
If M is a (right) comodule over the coalgebra C, then M is a (left) module over the dual algebra C∗, but the converse is not true in general: a module over C∗ is not necessarily a comodule over C. A rational comodule is a module over C∗ which becomes a comodule over C in the natural way.
References
- Gómez-Torrecillas, José (1998), "Coalgebras and comodules over a commutative ring", Revue Roumaine de Mathématiques Pures et Appliquées 43: 591–603
- Montgomery, Susan (1993). Hopf algebras and their actions on rings. Regional Conference Series in Mathematics 82. Providence, RI: American Mathematical Society. ISBN 0-8218-0738-2. Zbl 0793.16029.
This article is issued from Wikipedia - version of the Tuesday, November 24, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.