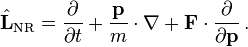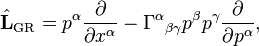Boltzmann equation
In physics, specifically non-equilibrium statistical mechanics, the Boltzmann equation or Boltzmann transport equation (BTE) describes the statistical behaviour of a thermodynamic system not in thermodynamic equilibrium. It was devised by Ludwig Boltzmann in 1872.[1] The classic example is a fluid with temperature gradients in space causing heat to flow from hotter regions to colder ones, by the random (and biased) transport of particles. In the modern literature the term Boltzmann equation is often used in a more general sense and refers to any kinetic equation that describes the change of a macroscopic quantity in a thermodynamic system, such as energy, charge or particle number.
The equation arises not by statistical analysis of all the individual positions and momenta of each particle in the fluid; rather by considering the probability that a number of particles all occupy a very small region of space (mathematically written d3r, where d means "differential", a very small change) centered at the tip of the position vector r, and have very nearly equal small changes in momenta from a momentum vector p, at an instant of time.
The Boltzmann equation can be used to determine how physical quantities change, such as heat energy and momentum, when a fluid is in transport, and other properties characteristic to fluids such as viscosity, thermal conductivity also electrical conductivity (by treating the charge carriers in a material as a gas) can be derived.[1] See also convection-diffusion equation.
The equation is a linear stochastic partial differential equation, since the unknown function in the equation is a continuous random variable. The problem of existence and uniqueness of solutions is still not fully resolved, but some recent results are quite promising.[2][3]
Overview
The phase space and density function
The set of all possible positions r and momenta p is called the phase space of the system; in other words a set of three coordinates for each position coordinate x, y, z, and three more for each momentum component px, py, pz. The entire space is 6-dimensional: a point in this space is (r, p) = (x, y, z, px, py, pz), and each coordinate is parameterized by time t. The small volume ("differential volume element") is written
Since the probability of N molecules which all have r and p within d3r d3p is in question, at the heart of the equation is a quantity f which gives this probability per unit phase-space volume, or probability per unit length cubed per unit momentum cubed, at an instant of time t. This is a probability density function: f(r, p, t), defined so that,
d3p is in question, at the heart of the equation is a quantity f which gives this probability per unit phase-space volume, or probability per unit length cubed per unit momentum cubed, at an instant of time t. This is a probability density function: f(r, p, t), defined so that,
is the number of molecules which all have positions lying within a volume element d3r about r and momenta lying within a momentum space element d3p about p, at time t.[4] Integrating over a region of position space and momentum space gives the total number of particles which have positions and momenta in that region:
which is a 6-fold integral. While f is associated with a number of particles, the phase space is for one-particle (not all of them, which is usually the case with deterministic many-body systems), since only one r and p is in question. It is not part of the analysis to use r1, p1 for particle 1, r2, p2 for particle 2, etc. up to rN, pN for particle N.
It is assumed the particles in the system are identical (so each has an identical mass m). For a mixture of more than one chemical species, one distribution is needed for each, see below.
Principal statement
The general equation can then be written:[5]
where the "force" term corresponds to the forces exerted on the particles by an external influence (not by the particles themselves), the "diff" term represents the diffusion of particles, and "coll" is the collision term - accounting for the forces acting between particles in collisions. Expressions for each term on the right side are provided below.[5]
Note that some authors use the particle velocity v instead of momentum p; they are related in the definition of momentum by p = mv.
The force and diffusion terms
Consider particles described by f, each experiencing an external force F not due to other particles (see the collision term for the latter treatment).
Suppose at time t some number of particles all have position r within element d3r and momentum p within d3p. If a force F instantly acts on each particle, then at time t + Δt their position will be r + Δr = r + pΔt/m and momentum p + Δp = p + FΔt. Then, in the absence of collisions, f must satisfy
Note that we have used the fact that the phase space volume element d3rd3p is constant, which can be shown using Hamilton's equations (see the discussion under Liouville's theorem). However, since collisions do occur, the particle density in the phase-space volume d3rd3p changes, so
-
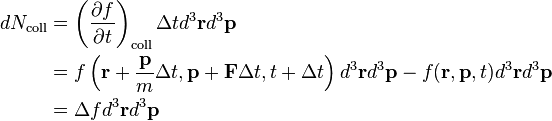
(1)
where Δf is the total change in f. Dividing (1) by d3rd3pΔt and taking the limits Δt → 0 and Δf → 0, we have
-
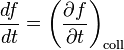
(2)
The total differential of f is:
-
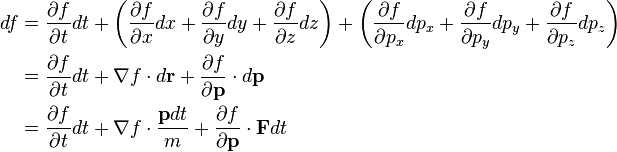
(3)
where ∇ is the gradient operator, · is the dot product,
is a shorthand for the momentum analogue of ∇, and êx, êy, êz are cartesian unit vectors.
Final statement
Dividing (3) by dt and substituting into (2) gives:
In this context, F(r, t) is the force field acting on the particles in the fluid, and m is the mass of the particles. The term on the right hand side is added to describe the effect of collisions between particles; if it is zero then the particles do not collide. The collisionless Boltzmann equation is often called the Vlasov equation.
This equation is more useful than the principal one above, yet still incomplete, since f cannot be solved unless the collision term in f is known. This term cannot be found as easily or generally as the others - it is a statistical term representing the particle collisions, and requires knowledge of the statistics the particles obey, like the Maxwell–Boltzmann, Fermi–Dirac or Bose–Einstein distributions.
The collision term (Stosszahlansatz) and molecular chaos
A key insight applied by Boltzmann was to determine the collision term resulting solely from two-body collisions between particles that are assumed to be uncorrelated prior to the collision. This assumption was referred to by Boltzmann as the "Stosszahlansatz", and is also known as the "molecular chaos assumption". Under this assumption the collision term can be written as a momentum-space integral over the product of one-particle distribution functions:[1]
where pA and pB are the momenta of any two particles (labeled as A and B for convenience) before a collision, p′A and p′B are the momenta after the collision,
is the magnitude of the relative momenta (see relative velocity for more on this concept), and I(g, Ω) is the differential cross section of the collision, in which the relative momenta of the colliding particles turns through an angle θ into the element of the solid angle dΩ, due to the collision.
Simplifications to the Boltzmann equation collision term
Since much of the challenge in solving the Boltzmann equation originates with the complex collision term, attempts have been made to 'model' and simplify the collision term. The best known model equation due to Bhatnagar, Gross and Krook.[6] The assumption in the BGK approximation is that the effect of molecular collisions is to force a non-equilibrium distribution function at a point in physical space back to a Maxwellian equilibrium distribution function and that the rate at which this occurs is proportional to the molecular collision frequency. The Boltzmann equation is therefore modified to the BGK form,
where 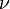 is the molecular collision frequency and
is the molecular collision frequency and  is the local Maxwellian distribution function given the gas temperature at this point in space.
is the local Maxwellian distribution function given the gas temperature at this point in space.
General equation (for a mixture)
For a mixture of chemical species labelled by indices i = 1,2,3...,n the equation for species i is:[1]
where fi = fi(r, pi, t), and the collision term is
where f′ = f′(p′i, t), the magnitude of the relative momenta is
and Iij is the differential cross-section as before, between particles i and j. The integration is over the momentum components in the integrand (which are labelled i and j). The sum of integrals describes the entry and exit of particles of species i in or out of the phase space element.
Applications and extensions
Conservation equations
The Boltzmann equation can be used to derive the fluid dynamic conservation laws for mass, charge, momentum and energy.[7]:p 163 For a fluid consisting of only one kind of particle, the number density n is given by:
The average value of any function A is:
Since the conservation equations involve tensors, the Einstein summation convention will be used where repeated indices in a product indicate summation over those indices. Thus 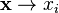 and
and 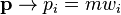 where
where  is the particle velocity vector. Define
is the particle velocity vector. Define 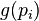 as some function of momentum
as some function of momentum  only, which is conserved in a collision. Assume also that the force
only, which is conserved in a collision. Assume also that the force  is a function of position only, and that f is zero for
is a function of position only, and that f is zero for 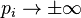 . Multiplying the Boltzmann equation by g and integrating over momentum yields four terms which, using integration by parts, can be expressed as:
. Multiplying the Boltzmann equation by g and integrating over momentum yields four terms which, using integration by parts, can be expressed as:
where the last term is zero since g is conserved in a collision. Letting 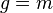 , the mass of the particle, the integrated Boltzmann equation becomes the conservation of mass equation:[7]:pp 12,168
, the mass of the particle, the integrated Boltzmann equation becomes the conservation of mass equation:[7]:pp 12,168
where 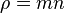 is the mass density and
is the mass density and 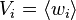 is the average fluid velocity.
is the average fluid velocity.
Letting 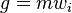 , the momentum of the particle, the integrated Boltzmann equation becomes the conservation of momentum equation:[7]:pp 15,169
, the momentum of the particle, the integrated Boltzmann equation becomes the conservation of momentum equation:[7]:pp 15,169
where 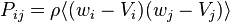 is the pressure tensor. (The viscous stress tensor plus the hydrostatic pressure.)
is the pressure tensor. (The viscous stress tensor plus the hydrostatic pressure.)
Letting 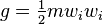 , the kinetic energy of the particle, the integrated Boltzmann equation becomes the conservation of energy equation:[7]:pp 19,169
, the kinetic energy of the particle, the integrated Boltzmann equation becomes the conservation of energy equation:[7]:pp 19,169
where 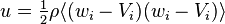 is the kinetic thermal energy density and
is the kinetic thermal energy density and 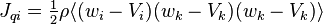 is the heat flux vector.
is the heat flux vector.
Hamiltonian mechanics
In Hamiltonian mechanics, the Boltzmann equation is often written more generally as
where L is the Liouville operator describing the evolution of a phase space volume and C is the collision operator. The non-relativistic form of L is
Quantum theory and violation of particle number
It is possible to write down Relativistic Boltzmann equations for relativistic quantum systems in which the number of particles is not conserved in collisions. This has several applications in physical cosmology,[8] including the formation of the light elements in big bang nucleosynthesis, the production of dark matter and baryogenesis. It is not a priori clear that the state of a quantum system can be characterized by a classical phase space density f. However, for a wide class of applications a well-defined generalization of f exists which is the solution of an effective Boltzmann equation that can be derived from first principles of quantum field theory.[9]
General relativity and astronomy
The Boltzmann equation is also often used in dynamics, especially galactic dynamics. A galaxy, under certain assumptions, may be approximated as a continuous fluid; its mass distribution is then represented by f; in galaxies, physical collisions between the stars are very rare, and the effect of gravitational collisions can be neglected for times far longer than the age of the universe.
The generalization to general relativity is
where Γαβγ is the Christoffel symbol of the second kind (this assumes there are no external forces, so that particles move along geodesics in the absence of collisions), with the important subtlety that the density is a function in mixed contravariant-covariant (xi, pi) phase space as opposed to fully contravariant (xi, pi) phase space.[10][11]
In physical cosmology, the study of processes in the early universe often requires to take into account the effects of quantum mechanics and general relativity.[8] In the very dense medium formed by the primordial plasma after the big bang particles are continuously created and annihilated. In such an environment quantum coherence and the spatial extension of the wavefunction can affect the dynamics, making it questionable whether the classical phase space distribution f that appears in the Boltzmann equation is suitable to describe the system. In many cases it is, however, possible to derive an effective Boltzmann equation for a generalized distribution function from first principles of quantum field theory.[9] This includes the formation of the light elements in big bang nucleosynthesis, the production of dark matter and baryogenesis.
Solution of the Boltzmann Equation
Until recently there were no known unique analytical solutions to the Boltzmann equation. However in 2010 mathematicians at the University of Pennsylvania[12] were able to use modern methods for solving partial differential equations and harmonic analysis to develop an analytical solution method and prove the global existence of classical solutions and rapid time decay to equilibrium for the Boltzmann equation with long-range interactions. Global existence and rapid decay imply that the equation correctly predicts that the solutions will continue to fit the system’s behavior and not undergo any mathematical catastrophes such as a breakdown of the equation’s integrity caused by a minor change within the equation. Rapid decay to equilibrium means that the effect of an initial small disturbance in the gas is short-lived and quickly becomes unnoticeable.
Until this breakthrough in analytical solution approaches, the various forms of the Boltzmann equation were solved using numerical methods to find approximate solutions to the various forms of the equation with applications ranging from hypersonic aerodynamics in rarefied gas flows[13] to plasma flows.[14]
See also
- Vlasov equation
- H-theorem
- Fokker–Planck equation
- Navier–Stokes equations
- Vlasov–Poisson equation
- Lattice Boltzmann methods
Notes
- 1 2 3 4 Encyclopaedia of Physics (2nd Edition), R.G. Lerner, G.L. Trigg, VHC publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3
- ↑ DiPerna, R. J.; Lions, P.-L. (1989). "On the Cauchy problem for Boltzmann equations: global existence and weak stability". Ann. Of Math. (2) 130 (2): 321–366. doi:10.2307/1971423.
- ↑ Philip T. Gressman and Robert M. Strain (2010). "Global classical solutions of the Boltzmann equation with long-range interactions". Proceedings of the National Academy of Sciences 107 (13): 5744–5749. arXiv:1002.3639. Bibcode:2010PNAS..107.5744G. doi:10.1073/pnas.1001185107.
- ↑ Huang, Kerson (1987). Statistical Mechanics (Second ed.). New York: Wiley. p. 53. ISBN 0-471-81518-7.
- 1 2 McGraw Hill Encyclopaedia of Physics (2nd Edition), C.B. Parker, 1994, ISBN 0-07-051400-3
- ↑ Bhatnagar, P. L.; Gross, E. P.; Krook, M. (1954-05-01). "A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems". Physical Review 94 (3): 511–525. doi:10.1103/PhysRev.94.511.
- 1 2 3 4 de Groot, S.R.; Mazur, P. (1984). Non-Equilibrium Thermodynamics. New York: Dover Publications Inc. ISBN 0-486-64741-2. Retrieved 2013-01-31.
- 1 2 Edward Kolb and Michael Turner (1990). The Early Universe. Westview Press. ISBN 9780201626742.
- 1 2 M. Drewes, C. Weniger, S. Mendizabal (8 January 2013). Phys. Lett. B 718 (3): 1119–1124. arXiv:1202.1301. Bibcode:2013PhLB..718.1119D. doi:10.1016/j.physletb.2012.11.046. Missing or empty
|title=(help) - ↑ Debbasch, Fabrice; Willem van Leeuwen (2009). "General relativistic Boltzmann equation I: Covariant treatment". Physica A 388 (7): 1079–1104. Bibcode:2009PhyA..388.1079D. doi:10.1016/j.physa.2008.12.023.
- ↑ Debbasch, Fabrice; Willem van Leeuwen (2009). "General relativistic Boltzmann equation II: Manifestly covariant treatment". Physica A 388 (9): 1818–34. Bibcode:2009PhyA..388.1818D. doi:10.1016/j.physa.2009.01.009.
- ↑ "Mathematicians Solve 140-Year-Old Boltzmann Equation". news.upenn.edu. Retrieved 2016-01-20.
- ↑ Evans, Ben; Morgan, Ken; Hassan, Oubay (2011-03-01). "A discontinuous finite element solution of the Boltzmann kinetic equation in collisionless and BGK forms for macroscopic gas flows". Applied Mathematical Modelling 35 (3): 996–1015. doi:10.1016/j.apm.2010.07.027.
- ↑ Pareschi, L.; Russo, G. (2000-01-01). "Numerical Solution of the Boltzmann Equation I: Spectrally Accurate Approximation of the Collision Operator". SIAM Journal on Numerical Analysis 37 (4): 1217–1245. doi:10.1137/S0036142998343300. ISSN 0036-1429.
References
- Harris, Stewart (1971). An introduction to the theory of the Boltzmann equation. Dover Books. p. 221. ISBN 978-0-486-43831-3.. Very unexpensive introduction to the modern framework (starting from a formal deduction from Liouville and BBGKY) in which the Bolrmann equation is placed. Most of statistical mechanics textbooks like Huang even threat the topic with the original arguments used by Boltzmann. For what concerns the deduction of the equation, these books rather use an heuristic explanation hiding the range of validity and the characteristic assumptions that distinguish Boltzmann's from other transport equations like Fokker-Planck or Landau equations.
- Arkeryd, Leif (1972). "On the Boltzmann equation part I: Existence". Arch. Rational Mech. Anal. 45: 1–16. Bibcode:1972ArRMA..45....1A. doi:10.1007/BF00253392.
- Arkeryd, Leif (1972). "On the Boltzmann equation part II: The full initial value problem". Arch. Rational Mech. Anal. 45: 17–34. Bibcode:1972ArRMA..45...17A. doi:10.1007/BF00253393.
- Arkeryd, Leif (1972). "On the Boltzmann equation part I: Existence". Arch. Rational Mech. Anal. 45: 1–16. Bibcode:1972ArRMA..45....1A. doi:10.1007/BF00253392.
- DiPerna, R. J.; Lions, P.-L. (1989). "On the Cauchy problem for Boltzmann equations: global existence and weak stability". Ann. Of Math. (2) 130: 321–366. doi:10.2307/1971423.
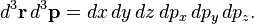
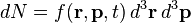
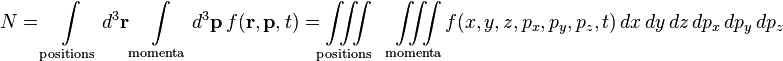
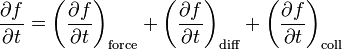
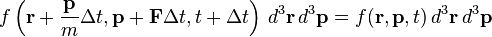
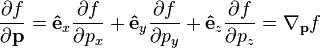
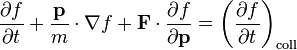
![\left(\frac{\partial f}{\partial t} \right)_{\mathrm{coll}} = \iint gI(g, \Omega)[f(\mathbf{p'}_A,t) f(\mathbf{p'}_B,t) - f(\mathbf{p}_A,t) f(\mathbf{p}_B,t)] \,d\Omega\,d^3\mathbf{p}_A\,d^3\mathbf{p}_B.](../I/m/9e6e6f2c6eb2a92e6332fc9c515b047e.png)
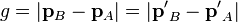
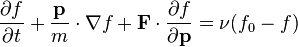
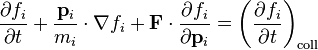
![\left(\frac{\partial f_i}{\partial t} \right)_{\mathrm{coll}} = \sum_{j=1}^n \iint g_{ij} I_{ij}(g_{ij}, \Omega)[f'_i f'_j - f_if_j] \,d\Omega\,d^3\mathbf{p'}.](../I/m/be25cffdaa1f202a7ca5091e5afb3d24.png)
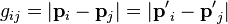
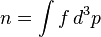
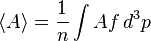
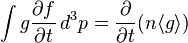
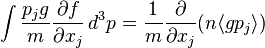
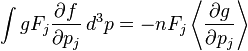
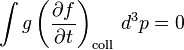
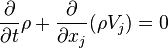
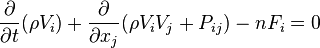
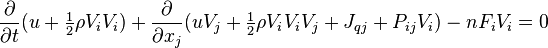
![\hat{\mathbf{L}}[f]=\mathbf{C}[f], \,](../I/m/34233ea8c7799c88886b88381d2c1961.png)