Cohomological dimension
In abstract algebra, cohomological dimension is an invariant of a group which measures the homological complexity of its representations. It has important applications in geometric group theory, topology, and algebraic number theory.
Cohomological dimension of a group
As most (co)homological invariants, the cohomological dimension involves a choice of a "ring of coefficients" R, with a prominent special case given by R = Z, the ring of integers. Let G be a discrete group, R a non-zero ring with a unit, and RG the group ring. The group G has cohomological dimension less than or equal to n, denoted cdR(G) ≤ n, if the trivial RG-module R has a projective resolution of length n, i.e. there are projective RG-modules P0, …, Pn and RG-module homomorphisms dk: Pk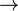 Pk − 1 (k = 1, …, n) and d0: P0
Pk − 1 (k = 1, …, n) and d0: P0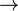 R, such that the image of dk coincides with the kernel of dk − 1 for k = 1, …, n and the kernel of dn is trivial.
R, such that the image of dk coincides with the kernel of dk − 1 for k = 1, …, n and the kernel of dn is trivial.
Equivalently, the cohomological dimension is less than or equal to n if for an arbitrary RG-module M, the cohomology of G with coeffients in M vanishes in degrees k > n, that is, Hk(G,M) = 0 whenever k > n. The p-cohomological dimension for prime p is similarly defined in terms of the p-torsion groups Hk(G,M){p}.[1]
The smallest n such that the cohomological dimension of G is less than or equal to n is the cohomological dimension of G (with coefficients R), which is denoted n = cdR(G).
A free resolution of Z can be obtained from a free action of the group G on a contractible topological space X. In particular, if X is a contractible CW complex of dimension n with a free action of a discrete group G that permutes the cells, then cdZ(G) ≤ n.
Examples
In the first group of examples, let the ring R of coefficients be Z.
- A free group has cohomological dimension one. As shown by John Stallings (for finitely generated group) and Richard Swan (in full generality), this property characterizes free groups.
- The fundamental group of a compact, connected, orientable Riemann surface other than the sphere has cohomological dimension two.
- More generally, the fundamental group of a compact, connected, orientable aspherical manifold of dimension n has cohomological dimension n. In particular, the fundamental group of a closed orientable hyperbolic n-manifold has cohomological dimension n.
- Nontrivial finite groups have infinite cohomological dimension over Z. More generally, the same is true for groups with nontrivial torsion.
Now let us consider the case of a general ring R.
- A group G has cohomological dimension 0 if and only if its group ring RG is semisimple. Thus a finite group has cohomological dimension 0 if and only if its order (or, equivalently, the orders of its elements) is invertible in R.
- Generalizing the Stallings–Swan theorem for R = Z, Dunwoody proved that a group has cohomological dimension at most one over an arbitrary ring R if and only if it is the fundamental group of a connected graph of finite groups whose orders are invertible in R.
Cohomological dimension of a field
The p-cohomological dimension of a field K is the p-cohomological dimension of the Galois group of a separable closure of K.[2] The cohomological dimension of K is the supremum of the p-cohomological dimension over all primes p.[3]
Examples
- Every field of non-zero characteristic "p" has "p"-cohomological dimension at most 1.[4]
- Every finite field has absolute Galois group isomorphic to
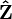 and so has cohomological dimension 1.[5]
and so has cohomological dimension 1.[5] - The field of formal Laurent series k((t)) over an algebraically closed field k of non-zero characteristic also has absolute Galois group isomorphic to
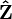 and so cohomological dimension 1.[5]
and so cohomological dimension 1.[5]
See also
References
- Brown, Kenneth S. (1994). Cohomology of groups. Graduate Texts in Mathematics 87 (Corrected reprint of the 1982 original ed.). New York: Springer-Verlag. ISBN 0-387-90688-6. MR 1324339. Zbl 0584.20036.
- Dicks, Warren (1980). Groups, Trees, and Projective Modules. Lecture Notes in Mathematics 790. Berlin: Springer-Verlag. doi:10.1007/BFb0088140. ISBN 3-540-09974-3. MR 0584790. Zbl 0427.20016.
- Dydak, Jerzy (2002). "Cohomological dimension theory". In Daverman, R. J. Handbook of geometric topology. Amsterdam: North-Holland. pp. 423–470. ISBN 0-444-82432-4. MR 1886675. Zbl 0992.55001.
- Gille, Philippe; Szamuely, Tamás (2006). Central simple algebras and Galois cohomology. Cambridge Studies in Advanced Mathematics 101. Cambridge: Cambridge University Press. ISBN 0-521-86103-9. Zbl 1137.12001.
- Serre, Jean-Pierre (1997). Galois cohomology. Springer-Verlag. ISBN 3-540-61990-9. Zbl 0902.12004.
- Shatz, Stephen S. (1972). Profinite groups, arithmetic, and geometry. Annals of Mathematics Studies 67. Princeton, NJ: Princeton University Press. ISBN 0-691-08017-8. MR 0347778. Zbl 0236.12002.
- Stallings, John R. (1968). "On torsion-free groups with infinitely many ends". Annals of Mathematics (2) 88: 312–334. doi:10.2307/1970577. ISSN 0003-486X. MR 0228573. Zbl 0238.20036.
- Swan, Richard G. (1969). "Groups of cohomological dimension one". Journal of Algebra 12: 585–610. doi:10.1016/0021-8693(69)90030-1. ISSN 0021-8693. MR 0240177. Zbl 0188.07001.