Coherent risk measure
In the fields of Actuarial Science and financial economics there are a number of ways that risk can be defined; to clarify the concept theoreticians have described a number of properties that a risk measure might or might not have. A coherent risk measure is a function 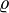 that satisfies properties of monotonicity, sub-additivity, homogeneity, and translational invariance.
that satisfies properties of monotonicity, sub-additivity, homogeneity, and translational invariance.
Properties
Consider a random outcome  viewed as an element of a linear space
viewed as an element of a linear space  of measurable functions, defined on an appropriate probability space. A functional
of measurable functions, defined on an appropriate probability space. A functional 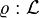 →
→ 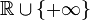 is said to be coherent risk measure for
is said to be coherent risk measure for  if it satisfies the following properties:[1]
if it satisfies the following properties:[1]
- Normalized
-
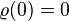
That is, the risk of holding no assets is zero.
- Monotonicity
-
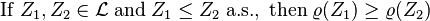
That is, if portfolio  always has better values than portfolio
always has better values than portfolio 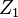 under almost all scenarios then the risk of
under almost all scenarios then the risk of  should be less than the risk of
should be less than the risk of 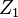 .[2] E.g. If
.[2] E.g. If 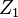 is an in the money call option (or otherwise) on a stock, and
is an in the money call option (or otherwise) on a stock, and  is also an in the money call option with a lower strike price.
is also an in the money call option with a lower strike price.
- Sub-additivity
-
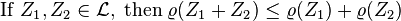
Indeed, the risk of two portfolios together cannot get any worse than adding the two risks separately: this is the diversification principle.
- Positive homogeneity
-
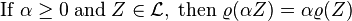
Loosely speaking, if you double your portfolio then you double your risk.
- Translation invariance
If  is a deterministic portfolio with guaranteed return
is a deterministic portfolio with guaranteed return  and
and 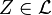 then
then
The portofolio  is just adding cash
is just adding cash  to your portfolio
to your portfolio 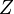 . In particular, if
. In particular, if 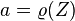 then
then 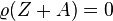 .
.
Convex risk measures
The notion of coherence has been subsequently relaxed. Indeed, the notions of Sub-additivity and Positive Homogeneity can be replaced by the notion of convexity:[3]
- Convexity
-
![\text{If }Z_1,Z_2 \in \mathcal{L}\text{ and }\lambda \in [0,1] \text{ then }\varrho(\lambda Z_1 + (1-\lambda) Z_2) \leq \lambda \varrho(Z_1) + (1-\lambda) \varrho(Z_2)](../I/m/bd8f75dc0d480230b8e83f2d2840db2b.png)
General framework of Wang transform
- Wang transform of the decumulative distribution function
A Wang transform of the decumulative distribution function is an increasing function ![g \colon [0,1] \rightarrow [0,1]](../I/m/1c5daa33c649dd0784f83c357260cec0.png) where
where 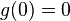 and
and 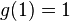 . [4] This function is called distortion function or Wang transform function.
. [4] This function is called distortion function or Wang transform function.
The dual distortion function is 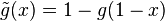 .[5][6]
Given a probability space
.[5][6]
Given a probability space 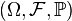 , then for any random variable
, then for any random variable  and any distortion function
and any distortion function  we can define a new probability measure
we can define a new probability measure 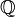 such that for any
such that for any 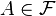 it follows that
it follows that
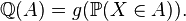 [5]
[5]
- Actuarial premium principle
For any increasing concave Wang transform function, we could define a corresponding premium principle :[4]
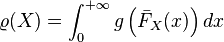
- Coherent risk measure
A coherent risk measure could be defined by a Wang transform of the decumulative distribution function  if on only if
if on only if  is concave.[4]
is concave.[4]
Examples of risk measure
Value at risk
It is well known that value at risk is not, in general, a coherent risk measure as it does not respect the sub-additivity property. An immediate consequence is that value at risk might discourage diversification.[1] Value at risk is, however, coherent, under the assumption of elliptically distributed losses (e.g. normally distributed) when the portfolio value is a linear function of the asset prices. However, in this case the value at risk becomes equivalent to a mean-variance approach where the risk of a portfolio is measured by the variance of the portfolio's return.
The Wang transform function (distortion function) for the Value at Risk is 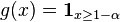 . The non-concavity of
. The non-concavity of  proves the non coherence of this risk measure.
proves the non coherence of this risk measure.
- Illustration
As a simple example to demonstrate the non-coherence of value-at-risk consider looking at the VaR of a portfolio at 95% confidence over the next year of two default-able zero coupon bonds that mature in 1 years time denominated in our numeraire currency.
Assume the following:
- The current yield on the two bonds is 0%
- The two bonds are from different issuers
- Each bonds has a 4% probability of defaulting over the next year
- The event of default in either bond is independent of the other
- Upon default the bonds have a recovery rate of 30%
Under these conditions the 95% VaR for holding either of the bonds is 0 since the probability of default is less than 5%. However if we held a portfolio that consisted of 50% of each bond by value then the 95% VaR is 35% (= 0.5*0.7 + 0.5*0) since the probability of at least one of the bonds defaulting is 7.84% which exceeds 5%. This violates the sub-additivity property showing that VaR is not a coherent risk measure.
Average value at risk
The average value at risk (sometimes called expected shortfall or conditional value-at-risk) is a coherent risk measure, even though it is derived from Value at Risk which is not.
Entropic value at risk
The entropic value at risk is a coherent risk measure.[7]
Tail value at risk
The tail value at risk (or tail conditional expectation) is a coherent risk measure only when the underlying distribution is continuous.
The Wang transform function (distortion function) for the tail value at risk is 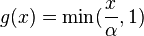 . The concavity of
. The concavity of  proves the coherence of this risk measure in the case of continuous distribution.
proves the coherence of this risk measure in the case of continuous distribution.
Proportional Hazard (PH) risk measure
The PH risk measure (or Proportional Hazard Risk measure) transforms the hasard rates 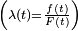 using a coefficient
using a coefficient  .
.
The Wang transform function (distortion function) for the PH risk measure is 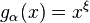 . The concavity of
. The concavity of  if
if 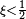 proves the coherence of this risk measure.
proves the coherence of this risk measure.

g-Entropic risk measures
g-entropic risk measures are a class of information-theoretic coherent risk measures that involve some important cases such as CVaR and EVaR.[7]
The Wang risk measure
The Wang risk measure is define by the following Wang transform function (distortion function) ![g_{\alpha}(x)=\Phi\left[ \Phi^{-1}(x)-\Phi^{-1}(\alpha)\right]](../I/m/3c139fdc52e138d4055f659aeb066c68.png) . The coherence of this risk measure is a consequence of the concavity of
. The coherence of this risk measure is a consequence of the concavity of  .
.
Entropic risk measure
The entropic risk measure is a convex risk measure which is not coherent. It is related to the exponential utility.
Superhedging price
The superhedging price is a coherent risk measure.
Set-valued
In a situation with  -valued portfolios such that risk can be measured in
-valued portfolios such that risk can be measured in 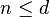 of the assets, then a set of portfolios is the proper way to depict risk. Set-valued risk measures are useful for markets with transaction costs.[8]
of the assets, then a set of portfolios is the proper way to depict risk. Set-valued risk measures are useful for markets with transaction costs.[8]
Properties
A set-valued coherent risk measure is a function  , where
, where  and
and  where
where  is a constant solvency cone and
is a constant solvency cone and  is the set of portfolios of the
is the set of portfolios of the  reference assets.
reference assets.  must have the following properties:[9]
must have the following properties:[9]
- Normalized
-

- Translative in M
-

- Monotone
-
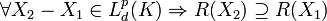
- Sublinear
Set-valued convex risk measure
If instead of the sublinear property,R is convex, then R is a set-valued convex risk measure.
Dual representation
A lower semi-continuous convex risk measure 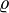 can be represented as
can be represented as
such that  is a penalty function and
is a penalty function and 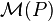 is the set of probability measures absolutely continuous with respect to P (the "real world" probability measure), i.e.
is the set of probability measures absolutely continuous with respect to P (the "real world" probability measure), i.e. 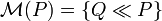 .
.
A lower semi-continuous risk measure is coherent if and only if it can be represented as
such that 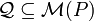 .[10]
.[10]
See also
- Risk metric - the abstract concept that a risk measure quantifies
- RiskMetrics - a model for risk management
- Spectral risk measure - a subset of coherent risk measures
- Distortion risk measure
- Conditional value-at-risk
- Entropic value at risk
- Financial risk
References
- 1 2 Artzner, P.; Delbaen, F.; Eber, J. M.; Heath, D. (1999). "Coherent Measures of Risk". Mathematical Finance 9 (3): 203. doi:10.1111/1467-9965.00068.
- ↑ Wilmott, P. (2006). "Quantitative Finance" 1 (2 ed.). Wiley: 342.
- ↑ Föllmer, H.; Schied, A. (2002). "Convex measures of risk and trading constraints". Finance and Stochastics 6 (4): 429–447. doi:10.1007/s007800200072.
- 1 2 3 Wang, Shuan (1996). "Premium Calculation by Transforming the Layer Premium Density". ASTIN Bulletin 26 (1): 71–92. doi:10.2143/ast.26.1.563234.
- 1 2 Balbás, A.; Garrido, J.; Mayoral, S. (2008). "Properties of Distortion Risk Measures". Methodology and Computing in Applied Probability 11 (3): 385. doi:10.1007/s11009-008-9089-z.
- ↑ Julia L. Wirch; Mary R. Hardy. "Distortion Risk Measures: Coherence and Stochastic Dominance" (pdf). Retrieved March 10, 2012.
- 1 2 Ahmadi-Javid, Amir (2012). "Entropic value-at-risk: A new coherent risk measure". Journal of Optimization Theory and Applications 155 (3): 1105–1123. doi:10.1007/s10957-011-9968-2.
- ↑ Jouini, Elyes; Meddeb, Moncef; Touzi, Nizar (2004). "Vector–valued coherent risk measures". Finance and Stochastics 8 (4): 531–552. doi:10.1007/s00780-004-0127-6.
- ↑ Hamel, A. H.; Heyde, F. (2010). "Duality for Set-Valued Measures of Risk" (pdf). SIAM Journal on Financial Mathematics 1 (1): 66–95. doi:10.1137/080743494. Retrieved August 17, 2012.
- ↑ Föllmer, Hans; Schied, Alexander (2004). Stochastic finance: an introduction in discrete time (2 ed.). Walter de Gruyter. ISBN 978-3-11-018346-7.
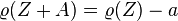
![\varrho(X) = \sup_{Q \in \mathcal{M}(P)} \{E^Q[-X] - \alpha(Q)\}](../I/m/9bdf71fcf7fd52bdd0663b54101da80d.png)
![\varrho(X) = \sup_{Q \in \mathcal{Q}} E^Q[-X]](../I/m/7e3a2934a9e7ce3b4153c105e1a79787.png)