Cofibration

In mathematics, in particular homotopy theory, a continuous mapping

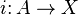i\colon A\to X

where A and X are topological spaces, is a cofibration if it satisfies the homotopy extension property with respect to all spaces Y. The name is because the dual condition, the homotopy lifting property, defines fibrations. For a more general notion of cofibration see the article about model categories.

Basic theorems

For Hausdorff spaces a cofibration is a closed inclusion (injective with closed image); for suitable spaces, a converse holds
Every map can be replaced by a cofibration via the mapping cylinder construction
There is a cofibration (A, X), if and only if there is a retraction from

X\times I

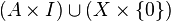(A\times I)\cup (X\times \{0\})

since this is the pushout and thus induces maps to every space sensible in the diagram.

Examples

Cofibrations are preserved under push-outs and composition, as one sees from the definition via diagram-chasing.
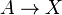A frequently used fact is that a cellular inclusion is a cofibration (so, for instance, if $(X,A)$ is a CW pair, then $A\to X$ is a cofibration). This follows from the previous fact since $S^{n-1}\to D^{n}$ is a cofibration for every $n$ .

References

Peter May, "A Concise Course in Algebraic Topology" : chapter 6 defines and discusses cofibrations, and they are used throughout

This article is issued from Wikipedia - version of the Saturday, December 12, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.