State space
In the theory of discrete dynamical systems, a state space is the set of values which a process can take. For example, a system in queueing theory recording the number of customers in a line would have state space {0, 1, 2, 3, ...}. State space is conceptually similar to phase space, but for discrete rather than continuous dynamical systems.
In a computer program, when the effective state space is small compared to all reachable states, this is referred to as clumping. Software such as LURCH analyzes such situations.
In games, the state space is the set of all possible configurations within the game. For instance, in backgammon, it consists of all the possible positions in which the 30 pieces can be placed, whether on the board, on the bar or in the bear-off tray. Within this state space there is the subset of positions which are valid according to the rules of backgammon. A game's total state space is often readily calculated whereas finding the subset of valid positions may be a considerable challenge. For example, a Chess board has 8x8=64 positions, and there are 32 distinct pieces, so by combination the total state space has 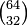 = 1,832,624,140,942,590,534 states.[1] However, most of those states are not valid positions.[2] The size of a game's state space is related to its complexity.
= 1,832,624,140,942,590,534 states.[1] However, most of those states are not valid positions.[2] The size of a game's state space is related to its complexity.
State space search explores a state space.
See also
- State space representation for information about continuous state space in control engineering.
- State space (physics) for information about continuous state space in physics.
- State space search
- State space planning
- Phase space for information about phase state (like continuous state space) in physics and mathematics.
- Probability space for information about state space in probability.
- Game complexity theory, which relies on the state space of game outcomes
- Dynamical systems for information about "state space" with a dynamical systems model of cognition.
References
- ↑ Chess.com http://www.chess.com/learn-how-to-play-chess. Retrieved 31 December 2014. Missing or empty
|title=(help) - ↑ Hamkins, Joel. MathOverflow http://mathoverflow.net/a/138499. Retrieved 31 December 2014. Missing or empty
|title=(help)
- Equivalence Relations on Finite Dynamical Systems, Laubenbacher, R. Pareigis, B., ADVANCES IN APPLIED MATHEMATICS, 2001, VOL 26; PART 3, pages 237–251
- State-space search: algorithms, complexity, extensions, and applications, Weixiong Zhang, Springer, 1999, ISBN 978-0-387-98832-0