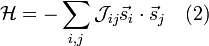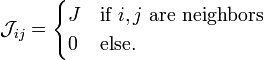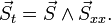Classical Heisenberg model

The Classical Heisenberg model is the $n = 3$ case of the n-vector model, one of the models used in statistical physics to model ferromagnetism, and other phenomena.

Definition

It can be formulated as follows: take a d-dimensional lattice, and a set of spins of the unit length

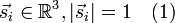\vec{s}_i \in \mathbb{R}^3, |\vec{s}_i|=1\quad (1)

each one placed on a lattice node.

The model is defined through the following Hamiltonian:

\mathcal{H} = -\sum_{i,j} \mathcal{J}_{ij} \vec{s}_i \cdot \vec{s}_j\quad (2)

with

\mathcal{J}_{ij} = \begin{cases} J & \mbox{if }i, j\mbox{ are neighbors} \\ 0 & \mbox{else.}\end{cases}

a coupling between spins.

Properties

The general mathematical formalism used to describe and solve the Heisenberg model and certain generalizations is developed in the article on the Potts model.

In the continuum limit the Heisenberg model (2) gives the following equation of motion

\vec{S}_{t}=\vec{S}\wedge \vec{S}_{xx}.

This equation is called the continuous classical Heisenberg ferromagnet equation or shortly Heisenberg model and is integrable in the soliton sense. It admits several integrable and nonintegrable generalizations like Landau-Lifshitz equation, Ishimori equation and so on.

One dimension

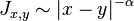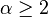In case of long range interaction, $J_{x,y}\sim |x-y|^{-\alpha}$ , the thermodynamic limit is well defined if $\alpha >1$ ; the magnetization remains zero if $\alpha \ge 2$ ; but the magnetization is positive, at low enough temperature, if 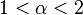$1< \alpha < 2$ (infrared bounds).

As in any 'nearest-neighbor' n-vector model with free boundary conditions, if the external field is zero, there exists a simple exact solution.

Two dimensions

In the case of long range interaction, 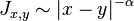$J_{x,y}\sim |x-y|^{-\alpha}$ , the thermodynamic limit is well defined if 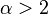$\alpha >2$ ; the magnetization remains zero if 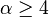$\alpha \ge 4$ ; but the magnetization is positive at low enough temperature if 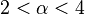$2< \alpha < 4$ (infrared bounds).

Polyakov has conjectured that, as opposed to the classical XY model, there is no dipole phase for any $T>0$ ; i.e. at non-zero temperature the correlations cluster exponentially fast.^[1]

Three and higher dimensions

Independently of the range of the interaction, at low enough temperature the magnetization is positive.

Conjecturally, in each of the low temperature extremal states the truncated correlations decay algebraically.

References

↑ Polyakov, A.M. (1975). "Interaction of goldstone particles in two dimensions. Applications to ferromagnets and massive Yang-Mills fields". Phys. Lett. B 59. Bibcode:1975PhLB...59...79P. doi:10.1016/0370-2693(75)90161-6.

External links

This article is issued from Wikipedia - version of the Saturday, September 12, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.