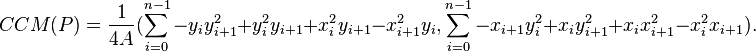Circumcenter of mass
In geometry, the circumcenter of mass is a center associated with a polygon which shares many of the properties of the center of mass. More generally, the circumcenter of mass may be defined for simplicial polytopes and also in the spherical and hyperbolic geometries.
In the special case when the polytope is a quadrilateral or hexagon, the circumcenter of mass has been called the "quasicircumcenter" and has been used to define an Euler line of a quadrilateral.[1][2] The circumcenter of mass allows us to define an Euler line for simplicial polytopes.
Definition in the plane
Let  be an oriented polygon (with vertices counted countercyclically) in the plane with vertices
be an oriented polygon (with vertices counted countercyclically) in the plane with vertices 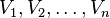 and let
and let  be an arbitrary point not lying on the sides (or their extensions). Consider the triangulation of
be an arbitrary point not lying on the sides (or their extensions). Consider the triangulation of  by the oriented triangles
by the oriented triangles 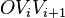 (the index
(the index  is viewed modulo
is viewed modulo  ). Associate with each of these triangles its circumcenter
). Associate with each of these triangles its circumcenter 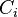 with weight equal to its oriented area (positive if its sequence of vertices is countercyclical; negative otherwise). The circumcenter of mass of
with weight equal to its oriented area (positive if its sequence of vertices is countercyclical; negative otherwise). The circumcenter of mass of  is the center of mass of these weighted circumcenters. The result is independent of the choice of point
is the center of mass of these weighted circumcenters. The result is independent of the choice of point 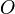 .[3]
.[3]

Properties
In the special case when the polygon is cyclic, the circumcenter of mass coincides with the circumcenter.
The circumcenter of mass satisfies an analog of Archimedes' Lemma, which states that if a polygon is decomposed into two smaller polygons, then the circumcenter of mass of that polygon is a weighted sum of the circumcenters of mass of the two smaller polygons. As a consequence, any triangulation with nondegenerate triangles may be used to define the circumcenter of mass.
For an equilateral polygon, the circumcenter of mass and center of mass coincide. More generally, the circumcenter of mass and center of mass coincide for a simplicial polytope for which each face has the sum of squares of its edges a constant.[4]
The circumcenter of mass is invariant under the operation of "recutting" of polygons.[5] and the discrete bicycle (Darboux) transformation; in other words, the image of a polygon under these operations has the same circumcenter of mass as the original polygon. The generalized Euler line makes other appearances in the theory of integrable systems.[6]
Let 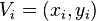 be the vertices of
be the vertices of  and let
and let  denote its area. The circumcenter of mass
denote its area. The circumcenter of mass 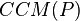 of the polygon
of the polygon  is given by the formula
is given by the formula
The circumcenter of mass can be extended to smooth curves via a limiting procedure. This continuous limit coincides with the center of mass of the homogeneous lamina bounded by the curve.
Under natural assumptions, the centers of polygons which satisfy Archimedes' Lemma are precisely the points of its Euler line. In other words, the only "well-behaved" centers which satisfy Archimedes' Lemma are the affine combinations of the circumcenter of mass and center of mass.
Generalized Euler line
The circumcenter of mass allows an Euler line to be defined for any polygon (and more generally, for a simplicial polytope). This generalized Euler line is defined as the affine span of the center of mass and circumcenter of mass of the polytope.
See also
References
- ↑ Myakishev, Alexei (2006), "On Two Remarkable Lines Related to a Quadrilateral" (PDF), Forum Geometricorum 6: 289–295.
- ↑ de Villiers, Michael (2014), "Quasi-circumcenters and a generalization of the quasi-Euler line to a hexagon" (PDF), Forum Geometricorum 14: 233–236
- ↑ Tabachnikov, Serge; Tsukerman, Emmanuel (May 2014), "Circumcenter of Mass and Generalized Euler Line", Discrete and Computational Geometry 51 (51): 815–836, doi:10.1007/s00454-014-9597-2
- ↑ Akopyan, Arseniy (May 2014), "Some Remarks on the Circumcenter of Mass", Discrete and Computational Geometry 51 (51): 837–841, doi:10.1007/s00454-014-9596-3
- ↑ Adler, V. (1993), "Cutting of polygons", Funct. Anal. Appl. (27): 141–143
- ↑ Schief, W. K. (2014), "Integrable structure in discrete shell membrane theory", Proceedings of The Royal Society of London. Series A. Mathematical, Physical and Engineering Sciences (470): 22