Choi–Williams distribution function

Choi–Williams distribution function is one of the members of Cohen's class distribution function.[1] It was first proposed by Hyung-Ill Choi and William J. Williams in 1989. This distribution function adopts exponential kernel to suppress the cross-term. However, the kernel gain does not decrease along the 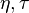\eta, \tau axes in the ambiguity domain. Consequently, the kernel function of Choi–Williams distribution function can only filter out the cross-terms that result from the components that differ in both time and frequency center.

Mathematical definition

The definition of the cone-shape distribution function is shown as follows:

C_x(t, f) = \int_{-\infty}^\infty \int_{-\infty}^\infty A_x(\eta,\tau) \Phi(\eta,\tau) \exp (j2\pi(\eta t-\tau f))\, d\eta\, d\tau,

where

A_x(\eta,\tau) = \int_{-\infty}^\infty x(t+\tau /2)x^*(t-\tau /2) e^{-j2\pi t\eta}\, dt,

and the kernel function is:

\Phi \left(\eta,\tau \right) = \exp \left[-\alpha \left(\eta \tau \right)^2 \right].

Following are the magnitude distribution of the kernel function in 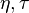\eta, \tau domain with different \alpha values.

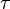As we can see from the figure above, the kernel function indeed suppress the interference which is away from the origin, but for the cross-term locates on the \eta and \tau axes, this kernel function can do nothing about it.

See also

References

  1. ↑ E. Sejdić, I. Djurović, J. Jiang, “Time-frequency feature representation using energy concentration: An overview of recent advances,” Digital Signal Processing, vol. 19, no. 1, pp. 153-183, January 2009.
This article is issued from Wikipedia - version of the Thursday, August 13, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.