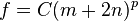Chladni's law

Chladni's law, named after Ernst Chladni, relates the frequency of modes of vibration for flat circular surfaces with fixed center as a function of the numbers m of diametric (linear) nodes and n of radial (circular) nodes. It is stated as the equation

f = C (m + 2n)^p \

where C and p are coefficients which depend on the properties of the plate.[1]

For flat circular plates, p is roughly 2, but Chladni's law can also be used to describe the vibrations of cymbals, handbells, and church bells in which case p can vary from 1.4 to 2.4.[2] In fact, p can even vary for a single object, depending on which family of modes is being examined.

References

  1. ↑ Rossing, Thomas D.; Fletcher, Neville H. (2004), Principles of Vibration and Sound, Springer, pp. 73–74, ISBN 9780387405568.
  2. ↑ Fletcher, Neville Horner; Rossing, Thomas D. (1998), The Physics of Musical Instruments, Springer, p. 680, ISBN 9780387983745.

External links


This article is issued from Wikipedia - version of the Friday, June 20, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.