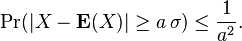Pafnuty Chebyshev

"Chebyshev" redirects here. For other uses, see Chebyshev (disambiguation).

Pafnuty Chebyshev
Pafnuty Lvovich Chebyshev
Born	(1821-05-16)May 16, 1821 Akatovo, Kaluga Governorate, Russian Empire
Died	December 8, 1894(1894-12-08) (aged 73) St. Petersburg, Russian Empire
Nationality	Russian
Fields	Mathematician
Institutions	St. Petersburg University
Alma mater	Moscow University
Doctoral advisor	Nikolai Brashman
Doctoral students	Dmitry Grave Aleksandr Korkin Aleksandr Lyapunov Andrey Markov Vladimir Andreevich Markov Konstantin Posse
Known for	probability, statistics, mechanics, and analytical geometry
Notable awards	Demidov Prize (1849)

Pafnuty Lvovich Chebyshev (Russian: Пафну́тий Льво́вич Чебышёв; IPA: [pɐfˈnutʲɪj ˈlʲvovʲɪtɕ tɕɪbɨˈʂof]) (May 16 [O.S. May 4] 1821 – December 8 [O.S. November 26] 1894)^[1] was a Russian mathematician. His name can be alternatively transliterated as Chebychev, Chebysheff, Chebyshov; or Tchebychev, Tchebycheff (French transcriptions); or Tschebyschev, Tschebyschef, Tschebyscheff (German transcriptions).

Biography

One of nine children, Chebyshev was born in the central Russian village of Akatovo near Borovsk, to Agrafena Ivanova Pozniakova and Lev Pavlovich Chebyshev. His father had fought as an officer against Napoleon Bonaparte's invading army.

Chebyshev was originally home schooled by his mother and his cousin, Avdotia Kvintillianova Soukhareva. He learned French early in life, which later helped him communicate with other mathematicians. A stunted leg prevented him from playing with other children, leading him to concentrate on his studies instead.

Chebyshev studied at the college level at Moscow University, where he earned his bachelor's degree in 1841. At Moscow University, Chebyshev was a graduate student of Nikolai Brashman.

After Chebyshev became a professor of mathematics in Moscow himself, his two most illustrious graduate students were Andrei Andreyevich Markov (the elder) and Aleksandr Lyapunov.

Later he moved to St. Petersburg, where he founded one of the most important schools of mathematics in Russia, and there is today a research institute in mathematics called the Chebyshev Laboratory in that city.

Mathematical contributions

Chebyshev is known for his work in the fields of probability, statistics, mechanics, and number theory. The Chebyshev inequality states that if $X$ is a random variable with standard deviation σ > 0, then the probability that the outcome of $X$ is no less than 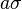$a\sigma$ away from its mean is no more than $1/a^2$ :

\Pr(|X - {\mathbf E}(X)| \ge a\,\sigma )\le \frac {1}{a^2}.

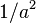The Chebyshev inequality is used to prove the Weak Law of Large Numbers.

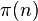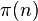The Bertrand–Chebyshev theorem (1845,1852) states that for any $n > 1$ , there exists a prime number $p$ such that $n < p < 2n$ . This is a consequence of the Chebyshev inequalities for the number $\pi(n)$ of prime numbers less than $n$ , which state that $\pi(n)$ is of the order of 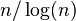$n/\log(n)$ . A more precise form is given by the celebrated prime number theorem: the quotient of the two expressions approaches 1.0 as $n$ tends to infinity.

Chebyshev is also known for the Chebyshev polynomials and the Chebyshev bias – the difference between the number of primes that are 3 (modulo 4) and 1 (modulo 4).

Legacy

Pafnuty Chebyshev on a stamp of the Soviet Union in 1946.

Chebyshev is considered to be a founding father of Russian mathematics. Among his well-known students were the mathematicians Dmitry Grave, Aleksandr Korkin, Aleksandr Lyapunov, and Andrei Markov. According to the Mathematics Genealogy Project, Chebyshev has 10,629 mathematical "descendants" as of 2015.^[2]

The lunar crater Chebyshev and the asteroid 2010 Chebyshev were named in his honour.

Publications

Tchebychef, P. L. (1899), Markov, Andreĭ Andreevich; Sonin, N., eds., Oeuvres I, New York: Commissionaires de l'Académie impériale des sciences, MR 0147353, Reprinted by Chelsea 1962
Tchebychef, P. L. (1907), Markov, Andreĭ Andreevich; Sonin, N., eds., Oeuvres II, New York: Commissionaires de l'Académie impériale des sciences, MR 0147353, Reprinted by Chelsea 1962
Butzer, P. L. Chebyshev (1821–1894): A Guide to his Life and Work, doi:10.1006/jath.1998.3289

References

External links

Mechanisms by Chebyshev – short 3d films – embodiment of Tchebishev's inventions
Pafnuty Chebyshev at the Mathematics Genealogy Project
O'Connor, John J.; Robertson, Edmund F., "Pafnuty Chebyshev", MacTutor History of Mathematics archive, University of St Andrews .
Works by or about Pafnuty Chebyshev in libraries (WorldCat catalog)
Biography, another one, and yet another (all in Russian).
Œuvres de P.L. Tchebychef (in French)

Authority control	WorldCat VIAF: 54930819 LCCN: n85344734 ISNI: 0000 0001 1886 3718 GND: 118666118 SELIBR: 180678 SUDOC: 07776255X BNF: cb13517018d (data) MGP: 12542 NLA: 35902887 NKC: ola2002159065 ICCU: IT\ICCU\CUBV\152195 RLS: 000082121

This article is issued from Wikipedia - version of the Sunday, January 31, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.