Alice and Bob

Alice and Bob are two commonly used placeholder names. They are used for archetypal characters in fields such as cryptography, game theory and physics.^[1] The names are used for convenience; for example, "Alice sends a message to Bob encrypted with his public key" is easier to follow than "Party A sends a message to Party B encrypted by Party B's public key." Following the alphabet, the specific names have evolved into common parlance within these fields—helping technical topics to be explained in a more understandable fashion.

Overview

These placeholder names are used for convenience and easier understanding. For example, if a writer wants to explain encrypted emails, the explanation might be:

1. Alice gets Bob's public key from the company directory.
2. Alice sends a message to Bob encrypted with Bob's public key.
3. Bob can use his secret key to unscramble it.

Every reader can intuitively figure out that they themselves could do the same thing as Bob or Alice.

In cryptography and computer security, there are a number of widely used names for the participants in discussions and presentations about various protocols.^[2] The names are conventional, somewhat self-suggestive, sometimes humorous, and effectively act as metasyntactic variables.

In typical implementations of these protocols, it is understood that the actions attributed to characters such as Alice or Bob need not always be carried out by human parties directly, but also by a trusted automated agent (such as a computer program) on their behalf.

Cast of characters

An example of an "Alice and Bob" analogy used in cryptography.

Alice and Bob diagram used to explain public-key cryptography.

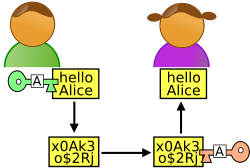
This list is drawn mostly from the book Applied Cryptography by Bruce Schneier. Alice and Bob are archetypes in cryptography; Eve is also common. Names further down the alphabet are less common.

• Alice and Bob. Generally, Alice wants to send a message to Bob. These names were used by Ron Rivest in the 1978 Communications of the ACM article presenting the RSA cryptosystem,^[3] and in A Method for Obtaining Digital Signatures and Public-Key Cryptosystems published April 4, 1977, revised September 1, 1977, as technical Memo LCS/TM82.
• Carol, Carlos or Charlie, as a third participant in communications.
• Chuck, as a third participant usually of malicious intent.^[4]
• Craig, the password cracker (usually encountered in situations with stored hashed/salted passwords).
• Dan or Dave, a fourth participant.
• Erin, a fifth participant. (Rarely used; E is usually reserved for Eve.)
• Eve, an eavesdropper, is usually a passive attacker. While she can listen in on messages between Alice and Bob, she cannot modify them. In quantum cryptography, Eve may also represent the environment.
• Faythe, a trusted advisor, courier or intermediary (repository of key service, courier of shared secrets. May be a machine role or human role; used infrequently. Faith or Faithful).
• Frank, a sixth participant (and so on alphabetically).
• Mallet^[5][6][7][8] or Mallory,^[9] a malicious attacker (less commonly called Trudy, an intruder); unlike the passive Eve, this one is the active man-in-the-middle attacker who can modify messages, substitute their own messages, replay old messages, and so on. The difficulty of securing a system against Mallet/Mallory is much greater than against Eve.
• Oscar, an opponent, similar to Mallet/Mallory but not necessarily malicious. Could be white-hat but still wants to crack, modify, substitute, or replay messages.
• Peggy, a prover, and Victor,^[9] a verifier, often must interact in some way to show that the intended transaction has actually taken place. They are often found in zero-knowledge proofs. Alternative names for the prover and the verifier are Pat and Vanna^[10] after Pat Sajak and Vanna White, the hosts of Wheel of Fortune.
• Sybil, an attacker who marshals a large number of pseudonymous identities, e.g. to subvert a reputation system. See Sybil attack.
• Trent, a trusted arbitrator, is some kind of neutral third party, whose exact role varies with the protocol under discussion.
• Walter, a warden, may be needed to guard Alice and Bob in some respect, depending on the protocol being discussed.
• Wendy, a whistleblower, is an insider with privileged access who may be in a position to divulge the information.

Although an interactive proof system is not quite a cryptographic protocol, it is sufficiently related to mention the cast of characters its literature features:

• Arthur and Merlin: In interactive proof systems, the prover has unbounded computational ability and is hence associated with Merlin, the powerful wizard from the Arthurian legend. He claims the truth of a statement, and Arthur, the wise king, questions him to verify the claim. These two characters also give the name for two complexity classes, namely MA and AM.
• A similar pair of characters is Paul and Carole. The characters were introduced in the solution of the Twenty Questions problem,^[11] where "Paul", who asked questions, stood for Paul Erdős and "Carole", who answered them, was an anagram of "oracle". They were further used in certain combinatorial games in the roles of Pusher and Chooser respectively, and have since been used in various roles.^[12]
• Arthur and Bertha are players in a combinatorial game. Arthur represents the "Left", "Black", or "Vertical" player. Bertha represents the "Right", "White", or "Horizontal" player. Additionally, Arthur, given the same outcome, prefers a game to take the fewest number of moves. Bertha likewise prefers a game to take the most number of moves.^[13]

See also

• Metasyntactic variable
• Placeholder name

References

Further reading

• C.H. Lindsey, Regulation of Investigatory Powers Bill: Some Scenarios, 2000

External links

• A Method for Obtaining Digital Signatures and Public-Key Cryptosystems
• The Alice and Bob After-Dinner Speech, given at the Zurich Seminar, April 1984, by John Gordon
• Geek Song: "Alice and Bob"
• Alice and Bob jokes (mainly Quantum Computing-related)
• Alice and Bob: IT's inseparable couple
• A short history of Bobs (story and slideshow) in the computing industry, from Alice & Bob to Microsoft Bob and Father of Ethernet Bob Metcalfe