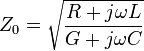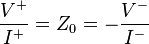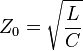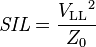Characteristic impedance

This article is about impedance in electrical circuits. For impedance of electromagnetic waves, see Wave impedance. For characteristic acoustic impedance, see Acoustic impedance.

A transmission line drawn as two black wires. At a distance x into the line, there is current phasor I(x) traveling through each wire, and there is a voltage difference phasor V(x) between the wires (bottom voltage minus top voltage). If

Z_0

is the characteristic impedance of the line, then

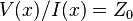V(x) / I(x) = Z_0

for a wave moving rightward, or

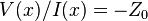V(x)/I(x) = -Z_0

for a wave moving leftward.

Schematic representation of a circuit where a source is coupled to a load with a transmission line having characteristic impedance

Z_0

The characteristic impedance or surge impedance (usually written Z₀) of a uniform transmission line is the ratio of the amplitudes of voltage and current of a single wave propagating along the line; that is, a wave travelling in one direction in the absence of reflections in the other direction. Characteristic impedance is determined by the geometry and materials of the transmission line and, for a uniform line, is not dependent on its length. The SI unit of characteristic impedance is the ohm.

The characteristic impedance of a lossless transmission line is purely real, with no reactive component. Energy supplied by a source at one end of such a line is transmitted through the line without being dissipated in the line itself. A transmission line of finite length (lossless or lossy) that is terminated at one end with an impedance equal to the characteristic impedance appears to the source like an infinitely long transmission line and produces no reflections.

Transmission line model

Schematic representation of an elemental length of a transmission line.

The characteristic impedance of a transmission line is the ratio of the voltage and current of a wave travelling along the line. When the wave reaches the end of the line, in general, there will be a reflected wave which travels back along the line in the opposite direction. When this wave reaches the source, it adds to the transmitted wave and the ratio of the voltage and current at the input to the line will no longer be the characteristic impedance. This new ratio is called the input impedance. The input impedance of an infinite line is equal to the characteristic impedance since the transmitted wave is never reflected back from the end. It can be shown that an equivalent definition is: the characteristic impedance of a line is that impedance which when terminating an arbitrary length of line at its output will produce an input impedance equal to the characteristic impedance. This is so because there is no reflection on a line terminated in its own characteristic impedance.

Applying the transmission line model based on the telegrapher's equations, the general expression for the characteristic impedance of a transmission line is:

Z_0=\sqrt{\frac{R+j\omega L}{G+j\omega C}}

where

R

is the resistance per unit length, considering the two conductors to be in series,

L

is the inductance per unit length,

G

is the conductance of the dielectric per unit length,

C

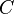is the capacitance per unit length,

j

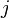is the imaginary unit, and

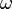\omega

is the angular frequency.

Although an infinite line is assumed, since all quantities are per unit length, the characteristic impedance is independent of the length of the transmission line.

The voltage and current phasors on the line are related by the characteristic impedance as:

\frac{V^+}{I^+} = Z_0 = -\frac{V^-}{I^-}

where the superscripts 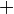$+$ and $-$ represent forward- and backward-traveling waves, respectively. A surge of energy on a finite transmission line will see an impedance of Z₀ prior to any reflections arriving, hence surge impedance is an alternative name for characteristic impedance.

Lossless line

The analysis of lossless lines provides an accurate approximation for real transmission lines that simplifies the mathematics considered in modeling transmission lines. A lossless line is defined as a transmission line that has no line resistance. This would imply that the line has infinite conductivity and acts like a perfect conductor. For a lossless line, R and G are both zero, so the equation for characteristic impedance derived above reduces to:

Z_0 = \sqrt{\frac{L}{C}}

The above expression is wholly real, since the imaginary term j has canceled out, implying that Z₀ is purely resistive. For a lossless line terminated in Z₀, there is no loss of current across the line, and so the voltage remains the same along the line. The lossless line model is a useful approximation for many practical cases, such as low-loss transmission lines and transmission lines with high frequency. For both of these cases, R and G are much smaller than ωL and ωC, respectively, and can thus be ignored.

Surge impedance loading

In electric power transmission, the characteristic impedance of a transmission line is expressed in terms of the surge impedance loading (SIL), or natural loading, being the power loading at which reactive power is neither produced nor absorbed:

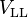\mathit{SIL}=\frac{{V_\mathrm{LL}}^2}{Z_0}

in which $V_\mathrm{LL}$ is the line-to-line voltage in volts.

Loaded below its SIL, a line supplies reactive power to the system, tending to raise system voltages. Above it, the line absorbs reactive power, tending to depress the voltage. The Ferranti effect describes the voltage gain towards the remote end of a very lightly loaded (or open ended) transmission line. Underground cables normally have a very low characteristic impedance, resulting in an SIL that is typically in excess of the thermal limit of the cable. Hence a cable is almost always a source of reactive power.

References

Guile, A. E. (1977). Electrical Power Systems. ISBN 0-08-021729-X.
Pozar, D. M. (February 2004). Microwave Engineering (3rd ed.). ISBN 0-471-44878-8.
Ulaby, F. T. (2004). Fundamentals Of Applied Electromagnetics (media ed.). Prentice Hall. ISBN 0-13-185089-X.

External links

This article incorporates public domain material from the General Services Administration document "Federal Standard 1037C".

This article is issued from Wikipedia - version of the Tuesday, December 08, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.