Chapman–Robbins bound
In statistics, the Chapman–Robbins bound or Hammersley–Chapman–Robbins bound is a lower bound on the variance of estimators of a deterministic parameter. It is a generalization of the Cramér–Rao bound; compared to the Cramér–Rao bound, it is both tighter and applicable to a wider range of problems. However, it is usually more difficult to compute.
The bound was independently discovered by John Hammersley in 1950,[1] and by Douglas Chapman and Herbert Robbins in 1951.[2]
Statement
Let θ ∈ Rn be an unknown, deterministic parameter, and let X ∈ Rk be a random variable, interpreted as a measurement of θ. Suppose the probability density function of X is given by p(x; θ). It is assumed that p(x; θ) is well-defined and that p(x; θ) > 0 for all values of x and θ.
Suppose δ(X) is an unbiased estimate of an arbitrary scalar function g: Rn → R of θ, i.e.,
The Chapman–Robbins bound then states that
Note that the denominator in the lower bound above is exactly the  -divergence of
-divergence of 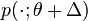 with respect to
with respect to 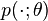 .
.
Relation to Cramér–Rao bound
The Chapman–Robbins bound converges to the Cramér–Rao bound when Δ → 0, assuming the regularity conditions of the Cramér–Rao bound hold. This implies that, when both bounds exist, the Chapman–Robbins version is always at least as tight as the Cramér–Rao bound; in many cases, it is substantially tighter.
The Chapman–Robbins bound also holds under much weaker regularity conditions. For example, no assumption is made regarding differentiability of the probability density function p(x; θ). When p(x; θ) is non-differentiable, the Fisher information is not defined, and hence the Cramér–Rao bound does not exist.
See also
References
- ↑ Hammersley, J. M. (1950), "On estimating restricted parameters", Journal of the Royal Statistical Society, Series B 12 (2): 192–240, JSTOR 2983981, MR 40631
- ↑ Chapman, D. G.; Robbins, H. (1951), "Minimum variance estimation without regularity assumptions", Annals of Mathematical Statistics 22 (4): 581–586, doi:10.1214/aoms/1177729548, JSTOR 2236927, MR 44084
Further reading
- Lehmann, E. L.; Casella, G. (1998), Theory of Point Estimation (2nd ed.), Springer, pp. 113–114, ISBN 0-387-98502-6
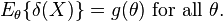
![\mathrm{Var}_{\theta}(\delta(X)) \ge \sup_\Delta \frac{\left[ g(\theta+\Delta) - g(\theta) \right]^2}{E_{\theta} \left[ \tfrac{p(X;\theta+\Delta)}{p(X;\theta)} - 1 \right]^2}.](../I/m/14e4d620c4c78a692cc7c180fffa8d4c.png)