Change of fiber

In algebraic topology, given a fibration p:E→B, the change of fiber is a map between the fibers induced by paths in B.

Since a covering is a fibration, the construction generalizes the corresponding facts in the theory of covering spaces.

Definition

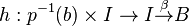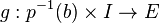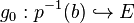If β is a path in B that starts at, say, b, then we have the homotopy $h: p^{-1}(b) \times I \to I \overset{\beta}\to B$ where the first map is a projection. Since p is a fibration, by the homotopy lifting property, h lifts to a homotopy $g: p^{-1}(b) \times I \to E$ with $g_0: p^{-1}(b) \hookrightarrow E$ . We have:

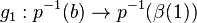g_1: p^{-1}(b) \to p^{-1}(\beta(1))

(There might be an ambiguity and so 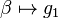$\beta \mapsto g_1$ need not be well-defined.)

Let 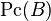$\operatorname{Pc}(B)$ denote the set of path classes in B. We claim that the construction determines the map:

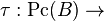\tau: \operatorname{Pc}(B) \to

the set of homotopy classes of maps.

Suppose β, β' are in the same path class; thus, there is a homotopy h from β to β'. Let

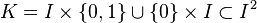K = I \times \{0, 1\} \cup \{0\} \times I \subset I^2

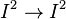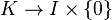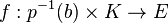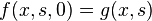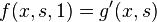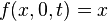Drawing a picture, there is a homeomorphism $I^2 \to I^2$ that restricts to a homeomorphism $K \to I \times \{0\}$ . Let $f: p^{-1}(b) \times K \to E$ be such that $f(x, s, 0) = g(x, s)$ , $f(x, s, 1) = g'(x, s)$ and $f(x, 0, t) = x$ .

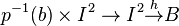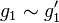Then, by the homotopy lifting property, we can lift the homotopy $p^{-1}(b) \times I^2 \to I^2 \overset{h}\to B$ to w such that w restricts to $f$ . In particular, we have $g_1 \sim g_1'$ , establishing the claim.

It is clear from the construction that the map is a homomorphism: if 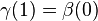$\gamma(1) =\beta(0)$ ,

\tau([c_b]) = \operatorname{id}, \, \tau([\beta] \cdot [\gamma]) = \tau([\beta]) \circ \tau([\gamma])

where 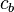$c_b$ is the constant path at b. It follows that $\tau([\beta])$ has inverse. Hence, we can actually say:

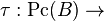\tau: \operatorname{Pc}(B) \to

the set of homotopy classes of homotopy equivalences.

Also, we have: for each b in B,

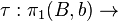\tau: \pi_1(B, b) \to

{ [ƒ] | homotopy equivalence

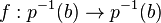f : p^{-1}(b) \to p^{-1}(b)

}

which is a group homomorphism (the right-hand side is clearly a group.) In other words, the fundamental group of B at b acts on the fiber over b, up to homotopy. This fact is a useful substitute for the absence of the structure group.

Consequence

One consequence of the construction is the below:

The fibers of p over a path-component is homotopy equivalent to each other.

References

James F. Davis, Paul Kirk, Lecture Notes in Algebraic Topology
May, J. A Concise Course in Algebraic Topology

This article is issued from Wikipedia - version of the Tuesday, January 26, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.