Centripetal Catmull–Rom spline
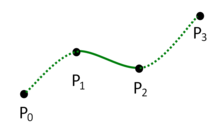
In computer graphics, centripetal Catmull–Rom spline is a variant form of Catmull-Rom spline [1] formulated according to the work of Barry and Goldman.[2] It is a type of interpolating spline (a curve that goes through its control points) defined by four control points 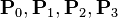 , with the curve drawn only from
, with the curve drawn only from 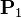 to
to 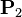 .
.
Definition
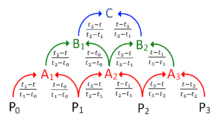

Let ![\mathbf{P}_i = [x_i \quad y_i]^T](../I/m/14e0ba735ca00e3bbc1a02fb435fe63e.png) denote a point. For a curve segment
denote a point. For a curve segment  defined by points
defined by points  and knot sequence
and knot sequence  , the centripetal Catmull-Rom spline can be produced by:
, the centripetal Catmull-Rom spline can be produced by:
where
and
in which  ranges from 0 to 1 for knot parameterization, and
ranges from 0 to 1 for knot parameterization, and 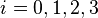 with
with 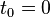 . For centripetal Catmull-Rom spline, the value of
. For centripetal Catmull-Rom spline, the value of  is
is 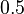 . When
. When 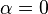 , the resulting curve is the standard Catmull-Rom spline (uniform Catmull-Rom spline); when
, the resulting curve is the standard Catmull-Rom spline (uniform Catmull-Rom spline); when  , the product is a chordal Catmull-Rom spline.
, the product is a chordal Catmull-Rom spline.
Plugging 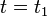 into the spline equations
into the spline equations 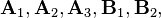 and
and 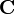 shows that the value of the spline curve at
shows that the value of the spline curve at  is
is 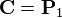 . Similarly, substituting
. Similarly, substituting 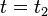 into the spline equations shows that
into the spline equations shows that 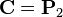 at
at  . This is true independent of the value of
. This is true independent of the value of  since the equation for
since the equation for 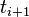 is not needed to calculate the value of
is not needed to calculate the value of 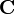 at points
at points 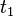 and
and  .
.
Advantages
Centripetal Catmull–Rom spline has several desirable mathematical properties compared to the original and the other types of Catmull-Rom formulation.[3] First, it will not form loop or self-intersection within a curve segment. Second, cusp will never occur within a curve segment. Third, it follows the control points more tightly.

Other uses
In computer vision, centripetal Catmull-Rom spline has been used to formulate an active model for segmentation. The method is termed active spline model.[4] The model is devised on the basis of active shape model, but uses centripetal Catmull-Rom spline to join two successive points (active shape model uses simple straight line), so that the total number of points necessary to depict a shape is lesser. The use of centripetal Catmull-Rom spline makes the training of a shape model much simpler, and it enables a better way to edit a contour after segmentation.
Code example
The following is an implementation of the Catmull–Rom spline in Python.
import numpy
import pylab as plt
def CatmullRomSpline(P0, P1, P2, P3, nPoints=100):
"""
P0, P1, P2, and P3 should be (x,y) point pairs that define the Catmull-Rom spline.
nPoints is the number of points to include in this curve segment.
"""
# Convert the points to numpy so that we can do array multiplication
P0, P1, P2, P3 = map(numpy.array, [P0, P1, P2, P3])
# Calculate t0 to t4
alpha = 0.5
def tj(ti, Pi, Pj):
xi, yi = Pi
xj, yj = Pj
return ( ( (xj-xi)**2 + (yj-yi)**2 )**0.5 )**alpha + ti
t0 = 0
t1 = tj(t0, P0, P1)
t2 = tj(t1, P1, P2)
t3 = tj(t2, P2, P3)
# Only calculate points between P1 and P2
t = numpy.linspace(t1,t2,nPoints)
# Reshape so that we can multiply by the points P0 to P3
# and get a point for each value of t.
t = t.reshape(len(t),1)
A1 = (t1-t)/(t1-t0)*P0 + (t-t0)/(t1-t0)*P1
A2 = (t2-t)/(t2-t1)*P1 + (t-t1)/(t2-t1)*P2
A3 = (t3-t)/(t3-t2)*P2 + (t-t2)/(t3-t2)*P3
B1 = (t2-t)/(t2-t0)*A1 + (t-t0)/(t2-t0)*A2
B2 = (t3-t)/(t3-t1)*A2 + (t-t1)/(t3-t1)*A3
C = (t2-t)/(t2-t1)*B1 + (t-t1)/(t2-t1)*B2
return C
def CatmullRomChain(P):
"""
Calculate Catmull Rom for a chain of points and return the combined curve.
"""
sz = len(P)
# The curve C will contain an array of (x,y) points.
C = []
for i in range(sz-3):
c = CatmullRomSpline(P[i], P[i+1], P[i+2], P[i+3])
C.extend(c)
return C
# Define a set of points for curve to go through
Points = [[0,1.5],[2,2],[3,1],[4,0.5],[5,1],[6,2],[7,3]]
# Calculate the Catmull-Rom splines through the points
c = CatmullRomChain(Points)
# Convert the Catmull-Rom curve points into x and y arrays and plot
x,y = zip(*c)
plt.plot(x,y)
# Plot the control points
px, py = zip(*Points)
plt.plot(px,py,'or')
plt.show()
See also
References
- ↑ E. Catmull and R. Rom. A class of local interpolating splines. Computer Aided Geometric Design, pages 317-326, 1974.
- ↑ P. J. Barry and R. N. Goldman. A recursive evaluation algorithm for a class of Catmull–Rom splines. SIGGRAPH Computer Graphics, 22(4):199-204, 1988.
- ↑ Yuksel, C.; Schaefer, S.; Keyser, J. (2011). "Parameterization and applications of Catmull-Rom curves". Computer-Aided Design 43: 747–755.
- ↑ Jen Hong, Tan; U. R., Acharya (2014). "Active spline model: A shape based model—interactive segmentation". Digital Signal Processing 35: 64–74.
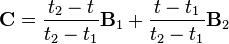
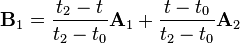
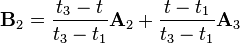
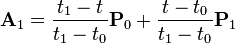
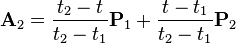
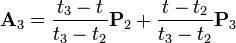
![t_{i+1} = \left[\sqrt{(x_{i+1}-x_i)^2+(y_{i+1}-y_i)^2}\right]^{\alpha} + t_i](../I/m/fe7b74f6eaf0d43c1fb8c7e8daba64b8.png)