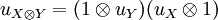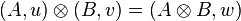Center (category theory)

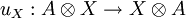Let $\mathcal{C} = (\mathcal{C},\otimes,I)$ be a (strict) monoidal category. The center of $\mathcal{C}$ , also called the Drinfeld center of $\mathcal{C}$ ^[1] and denoted $\mathcal{Z(C)}$ , is the category whose objects are pairs (A,u) consisting of an object A of $\mathcal{C}$ and a natural isomorphism $u_X:A \otimes X \rightarrow X \otimes A$ satisfying

u_{X \otimes Y} = (1 \otimes u_Y)(u_X \otimes 1)

and

u_I = 1_A

(this is actually a consequence of the first axiom).

An arrow from (A,u) to (B,v) in $\mathcal{Z(C)}$ consists of an arrow $f:A \rightarrow B$ in $\mathcal{C}$ such that

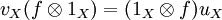v_X (f \otimes 1_X) = (1_X \otimes f) u_X

The category $\mathcal{Z(C)}$ becomes a braided monoidal category with the tensor product on objects defined as

(A,u) \otimes (B,v) = (A \otimes B,w)

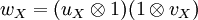where $w_X = (u_X \otimes 1)(1 \otimes v_X)$ , and the obvious braiding .

References

↑ Majid 1991.

Joyal, André; Street, Ross (1991), "Tortile Yang-Baxter operators in tensor categories", Journal of Pure and Applied Algebra 71 (1): 43–51, doi:10.1016/0022-4049(91)90039-5, MR 1107651 .
Majid, Shahn (1991). "Representations, duals and quantum doubles of monoidal categories". Proceedings of the Winter School on Geometry and Physics (Srní, 1990). Rendiconti del Circolo Matematico di Palermo. Serie II. Supplemento (26). pp. 197–206. MR 1151906.
Drinfeld center in nLab

This article is issued from Wikipedia - version of the Monday, October 19, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.