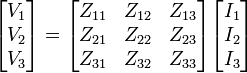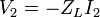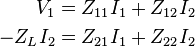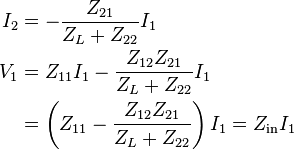Two-port network
A two-port network (a kind of four-terminal network or quadripole) is an electrical network (circuit) or device with two pairs of terminals to connect to external circuits. Two terminals constitute a port if the currents applied to them satisfy the essential requirement known as the port condition: the electric current entering one terminal must equal the current emerging from the other terminal on the same port.[1][2] The ports constitute interfaces where the network connects to other networks, the points where signals are applied or outputs are taken. In a two-port network, often port 1 is considered the input port and port 2 is considered the output port.
The two-port network model is used in mathematical circuit analysis techniques to isolate portions of larger circuits. A two-port network is regarded as a "black box" with its properties specified by a matrix of numbers. This allows the response of the network to signals applied to the ports to be calculated easily, without solving for all the internal voltages and currents in the network. It also allows similar circuits or devices to be compared easily. For example, transistors are often regarded as two-ports, characterized by their h-parameters (see below) which are listed by the manufacturer. Any linear circuit with four terminals can be regarded as a two-port network provided that it does not contain an independent source and satisfies the port conditions.
Examples of circuits analyzed as two-ports are filters, matching networks, transmission lines, transformers, and small-signal models for transistors (such as the hybrid-pi model). The analysis of passive two-port networks is an outgrowth of reciprocity theorems first derived by Lorentz.[3]
In two-port mathematical models, the network is described by a 2 by 2 square matrix of complex numbers. The common models that are used are referred to as z-parameters, y-parameters, h-parameters, g-parameters, and ABCD-parameters, each described individually below. These are all limited to linear networks since an underlying assumption of their derivation is that any given circuit condition is a linear superposition of various short-circuit and open circuit conditions. They are usually expressed in matrix notation, and they establish relations between the variables
 , voltage across port 1
, voltage across port 1 , current into port 1
, current into port 1 , voltage across port 2
, voltage across port 2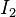 , current into port 2
, current into port 2
which are shown in figure 1. The difference between the various models lies in which of these variables are regarded as the independent variables. These current and voltage variables are most useful at low-to-moderate frequencies. At high frequencies (e.g., microwave frequencies), the use of power and energy variables is more appropriate, and the two-port current–voltage approach is replaced by an approach based upon scattering parameters.
General properties
There are certain properties of two-ports that frequently occur in practical networks and can be used to greatly simplify the analysis. These include:
- Reciprocal networks
- A network is said to be reciprocal if the voltage appearing at port 2 due to a current applied at port 1 is the same as the voltage appearing at port 1 when the same current is applied to port 2. Exchanging voltage and current results in an equivalent definition of reciprocity. A network that consists entirely of linear passive components (that is, resistors, capacitors and inductors) is usually reciprocal, a notable exception being passive circulators and isolators that contain magnetized materials. In general, it will not be reciprocal if it contains active components such as generators or transistors.[4]
- Symmetrical networks
- A network is symmetrical if its input impedance is equal to its output impedance. Most often, but not necessarily, symmetrical networks are also physically symmetrical. Sometimes also antimetrical networks are of interest. These are networks where the input and output impedances are the duals of each other.[5]
- Lossless network
- A lossless network is one which contains no resistors or other dissipative elements.[6]
Impedance parameters (z-parameters)
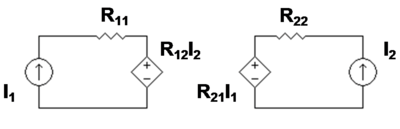
where
Notice that all the z-parameters have dimensions of ohms.
For reciprocal networks  . For symmetrical networks
. For symmetrical networks 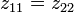 . For reciprocal lossless networks all the
. For reciprocal lossless networks all the 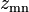 are purely imaginary.[7]
are purely imaginary.[7]
Example: bipolar current mirror with emitter degeneration
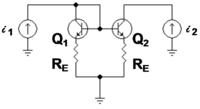

Figure 3 shows a bipolar current mirror with emitter resistors to increase its output resistance.[nb 1] Transistor Q1 is diode connected, which is to say its collector-base voltage is zero. Figure 4 shows the small-signal circuit equivalent to Figure 3. Transistor Q1 is represented by its emitter resistance rE ≈ VT / IE (VT = thermal voltage, IE = Q-point emitter current), a simplification made possible because the dependent current source in the hybrid-pi model for Q1 draws the same current as a resistor 1 / gm connected across rπ. The second transistor Q2 is represented by its hybrid-pi model. Table 1 below shows the z-parameter expressions that make the z-equivalent circuit of Figure 2 electrically equivalent to the small-signal circuit of Figure 4.
| Expression | Approximation | |
|---|---|---|
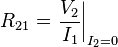 |
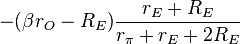 |
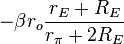 |
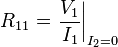 |
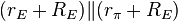 [nb 2] [nb 2] |
|
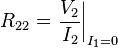 |
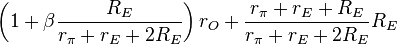 |
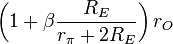 |
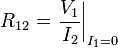 |
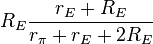 |
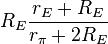 |
The negative feedback introduced by resistors RE can be seen in these parameters. For example, when used as an active load in a differential amplifier, I1 ≈ −I2, making the output impedance of the mirror approximately R22 -R21 ≈ 2 β rORE /(rπ + 2RE) compared to only rO without feedback (that is with RE = 0 Ω) . At the same time, the impedance on the reference side of the mirror is approximately R11 − R12 ≈ 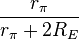
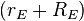 , only a moderate value, but still larger than rE with no feedback. In the differential amplifier application, a large output resistance increases the difference-mode gain, a good thing, and a small mirror input resistance is desirable to avoid Miller effect.
, only a moderate value, but still larger than rE with no feedback. In the differential amplifier application, a large output resistance increases the difference-mode gain, a good thing, and a small mirror input resistance is desirable to avoid Miller effect.
Admittance parameters (y-parameters)
where
Notice that all the Y-parameters have dimensions of siemens.
For reciprocal networks 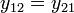 . For symmetrical networks
. For symmetrical networks 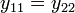 . For reciprocal lossless networks all the
. For reciprocal lossless networks all the 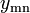 are purely imaginary.[7]
are purely imaginary.[7]
Hybrid parameters (h-parameters)
where
This circuit is often selected when a current amplifier is wanted at the output. The resistors shown in the diagram can be general impedances instead.
Notice that off-diagonal h-parameters are dimensionless, while diagonal members have dimensions the reciprocal of one another.
Example: common-base amplifier
Note: Tabulated formulas in Table 2 make the h-equivalent circuit of the transistor from Figure 6 agree with its small-signal low-frequency hybrid-pi model in Figure 7. Notation: rπ = base resistance of transistor, rO = output resistance, and gm = transconductance. The negative sign for h21 reflects the convention that I1, I2 are positive when directed into the two-port. A non-zero value for h12 means the output voltage affects the input voltage, that is, this amplifier is bilateral. If h12 = 0, the amplifier is unilateral.
| Expression | Approximation | |
|---|---|---|
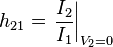 |
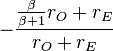 |
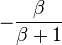 |
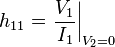 |
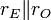 |
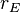 |
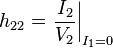 |
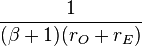 |
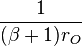 |
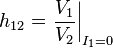 |
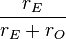 |
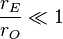 |
Inverse hybrid parameters (g-parameters)
where
Often this circuit is selected when a voltage amplifier is wanted at the output. Notice that off-diagonal g-parameters are dimensionless, while diagonal members have dimensions the reciprocal of one another. The resistors shown in the diagram can be general impedances instead.
Example: common-base amplifier
Note: Tabulated formulas in Table 3 make the g-equivalent circuit of the transistor from Figure 8 agree with its small-signal low-frequency hybrid-pi model in Figure 9. Notation: rπ = base resistance of transistor, rO = output resistance, and gm = transconductance. The negative sign for g12 reflects the convention that I1, I2 are positive when directed into the two-port. A non-zero value for g12 means the output current affects the input current, that is, this amplifier is bilateral. If g12 = 0, the amplifier is unilateral.
| Expression | Approximation | |
|---|---|---|
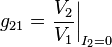 |
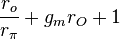 |
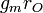 |
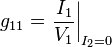 |
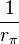 |
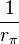 |
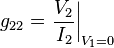 |
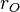 |
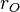 |
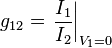 |
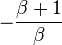 |
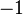 |
ABCD-parameters
The ABCD-parameters are known variously as chain, cascade, or transmission line parameters. There are a number of definitions given for ABCD parameters, the most common is,[8][9]
For reciprocal networks 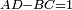 . For symmetrical networks
. For symmetrical networks 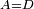 . For networks which are reciprocal and lossless, A and D are purely real while B and C are purely imaginary.[6]
. For networks which are reciprocal and lossless, A and D are purely real while B and C are purely imaginary.[6]
This representation is preferred because when the parameters are used to represent a cascade of two-ports, the matrices are written in the same order that a network diagram would be drawn, that is, left to right. However, the examples given below are based on a variant definition;
where
The negative signs in the definitions of parameters 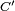 and
and 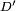 arise because
arise because 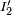 is defined with the opposite sense to
is defined with the opposite sense to 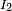 , that is,
, that is, 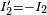 . The reason for adopting this convention is so that the output current of one cascaded stage is equal to the input current of the next. Consequently, the input voltage/current matrix vector can be directly replaced with the matrix equation of the preceding cascaded stage to form a combined
. The reason for adopting this convention is so that the output current of one cascaded stage is equal to the input current of the next. Consequently, the input voltage/current matrix vector can be directly replaced with the matrix equation of the preceding cascaded stage to form a combined 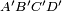 matrix.
matrix.
The terminology of representing the 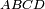 parameters as a matrix of elements designated a11 etc. as adopted by some authors[10] and the inverse
parameters as a matrix of elements designated a11 etc. as adopted by some authors[10] and the inverse 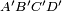 parameters as a matrix of elements designated b11 etc. is used here for both brevity and to avoid confusion with circuit elements.
parameters as a matrix of elements designated b11 etc. is used here for both brevity and to avoid confusion with circuit elements.
An ABCD matrix has been defined for Telephony four-wire Transmission Systems by P K Webb in British Post Office Research Department Report 630 in 1977.
Table of transmission parameters
The table below lists ABCD and inverse ABCD parameters for some simple network elements.
| Element | [a] matrix | [b] matrix | Remarks |
|---|---|---|---|
| Series resistor | 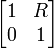 |
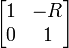 |
R, resistance |
| Shunt resistor | 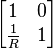 |
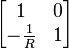 |
R, resistance |
| Series conductor | 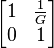 |
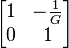 |
G, conductance |
| Shunt conductor | 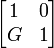 |
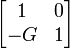 |
G, conductance |
| Series inductor | 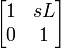 |
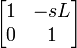 |
L, inductance s, complex angular frequency |
| Shunt capacitor | 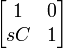 |
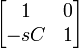 |
C, capacitance s, complex angular frequency |
| Series capacitor | 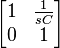 |
C, capacitance s, complex angular frequency | |
| Transmission line | 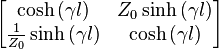 |
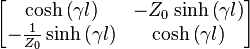 [11] [11] |
Z0, characteristic impedance γ, propagation constant ( 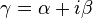 ) )l, length of transmission line (m) |
Scattering parameters (S-parameters)
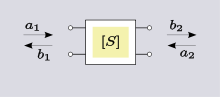
The previous parameters are all defined in terms of voltages and currents at ports. S-parameters are different, and are defined in terms of incident and reflected waves at ports. S-parameters are used primarily at UHF and microwave frequencies where it becomes difficult to measure voltages and currents directly. On the other hand, incident and reflected power are easy to measure using directional couplers. The definition is,[12]
where the  are the incident waves and the
are the incident waves and the  are the reflected waves at port k. It is conventional to define the
are the reflected waves at port k. It is conventional to define the  and
and  in terms of the square root of power. Consequently, there is a relationship with the wave voltages (see main article for details).[13]
in terms of the square root of power. Consequently, there is a relationship with the wave voltages (see main article for details).[13]
For reciprocal networks 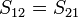 . For symmetrical networks
. For symmetrical networks 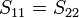 . For antimetrical networks
. For antimetrical networks 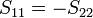 .[14] For lossless reciprocal networks
.[14] For lossless reciprocal networks 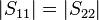 and
and 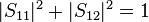 .[15]
.[15]
Scattering transfer parameters (T-parameters)
Scattering transfer parameters, like scattering parameters, are defined in terms of incident and reflected waves. The difference is that T-parameters relate the waves at port 1 to the waves at port 2 whereas S-parameters relate the reflected waves to the incident waves. In this respect T-parameters fill the same role as ABCD parameters and allow the T-parameters of cascaded networks to be calculated by matrix multiplication of the component networks. T-parameters, like ABCD parameters, can also be called transmission parameters. The definition is,[12][16]
T-parameters are not so easy to measure directly unlike S-parameters. However, S-parameters are easily converted to T-parameters, see main article for details.[17]
Combinations of two-port networks
When two or more two-port networks are connected, the two-port parameters of the combined network can be found by performing matrix algebra on the matrices of parameters for the component two-ports. The matrix operation can be made particularly simple with an appropriate choice of two-port parameters to match the form of connection of the two-ports. For instance, the z-parameters are best for series connected ports.
The combination rules need to be applied with care. Some connections (when dissimilar potentials are joined) result in the port condition being invalidated and the combination rule will no longer apply. This difficulty can be overcome by placing 1:1 ideal transformers on the outputs of the problem two-ports. This does not change the parameters of the two-ports, but does ensure that they will continue to meet the port condition when interconnected. An example of this problem is shown for series-series connections in figures 11 and 12 below.[18]
Series-series connection

When two-ports are connected in a series-series configuration as shown in figure 10, the best choice of two-port parameter is the z-parameters. The z-parameters of the combined network are found by matrix addition of the two individual z-parameter matrices.[19][20]


As mentioned above, there are some networks which will not yield directly to this analysis.[18] A simple example is a two-port consisting of a L-network of resistors R1 and R2. The z-parameters for this network are;
Figure 11 shows two identical such networks connected in series-series. The total z-parameters predicted by matrix addition are;
However, direct analysis of the combined circuit shows that,
The discrepancy is explained by observing that R1 of the lower two-port has been by-passed by the short-circuit between two terminals of the output ports. This results in no current flowing through one terminal in each of the input ports of the two individual networks. Consequently, the port condition is broken for both the input ports of the original networks since current is still able to flow into the other terminal. This problem can be resolved by inserting an ideal transformer in the output port of at least one of the two-port networks. While this is a common text-book approach to presenting the theory of two-ports, the practicality of using transformers is a matter to be decided for each individual design.
Parallel-parallel connection

When two-ports are connected in a parallel-parallel configuration as shown in figure 13, the best choice of two-port parameter is the y-parameters. The y-parameters of the combined network are found by matrix addition of the two individual y-parameter matrices.[21]
Series-parallel connection

When two-ports are connected in a series-parallel configuration as shown in figure 14, the best choice of two-port parameter is the h-parameters. The h-parameters of the combined network are found by matrix addition of the two individual h-parameter matrices.[22]
Parallel-series connection
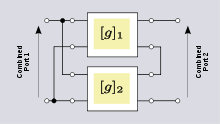
When two-ports are connected in a parallel-series configuration as shown in figure 15, the best choice of two-port parameter is the g-parameters. The g-parameters of the combined network are found by matrix addition of the two individual g-parameter matrices.
Cascade connection
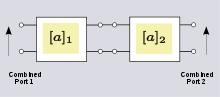
When two-ports are connected with the output port of the first connected to the input port of the second (a cascade connection) as shown in figure 16, the best choice of two-port parameter is the ABCD-parameters. The a-parameters of the combined network are found by matrix multiplication of the two individual a-parameter matrices.[23]
A chain of n two-ports may be combined by matrix multiplication of the n matrices. To combine a cascade of b-parameter matrices, they are again multiplied, but the multiplication must be carried out in reverse order, so that;
Example
Suppose we have a two-port network consisting of a series resistor R followed by a shunt capacitor C. We can model the entire network as a cascade of two simpler networks:
The transmission matrix for the entire network 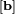 is simply the matrix multiplication of the transmission matrices for the two network elements:
is simply the matrix multiplication of the transmission matrices for the two network elements:
Thus:
Interrelation of parameters
![\mathbf{[z]}](../I/m/41884dfd23f60b539a04d59ff5d4aa0e.png) |
![\mathbf{[y]}](../I/m/769226a5d0073e17f4e3e17ab0c40ea9.png) |
![\mathbf{[h]}](../I/m/dd88b463c4a0fd1740f49a6375ee2a42.png) |
![\mathbf{[g]}](../I/m/a9566d52f3fe1ec530e00304f257b143.png) |
![\mathbf{[a]}](../I/m/46fb6e8076edcdfcc2bdc7bd547257b1.png) |
![\mathbf{[b]}](../I/m/499e8b0761e9aa846009e894b6fd52d3.png) | |
|---|---|---|---|---|---|---|
![\mathbf{[z]}](../I/m/41884dfd23f60b539a04d59ff5d4aa0e.png) |
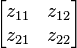 |
![\frac{1}{\Delta \mathbf{[y]}} \begin{bmatrix} y_{22} & -y_{12} \\ -y_{21} & y_{11} \end{bmatrix}](../I/m/5d08a6aef184d2a4a18bf0d4b948393d.png) |
![\frac{1}{h_{22}} \begin{bmatrix} \Delta \mathbf{[h]} & h_{12} \\ -h_{21} & 1 \end{bmatrix}](../I/m/18b51bedd630f18fcb84bd1f2a7b95dd.png) |
![\frac{1}{g_{11}} \begin{bmatrix} 1 & -g_{12} \\ g_{21} & \Delta \mathbf{[g]} \end{bmatrix}](../I/m/ca12ecc6e8ee7c7024725d4d51600350.png) |
![\frac{1}{a_{21}} \begin{bmatrix} a_{11} & \Delta \mathbf{[a]} \\ 1 & a_{22} \end{bmatrix}](../I/m/2fdbb0c91a7301f2b9b24a44890207fa.png) |
![\frac{1}{b_{21}} \begin{bmatrix} -b_{22} & -1 \\ -\Delta \mathbf{[b]} & -b_{11} \end{bmatrix}](../I/m/0f83203937f67c6728de6d6da74eec84.png) |
![\mathbf{[y]}](../I/m/769226a5d0073e17f4e3e17ab0c40ea9.png) |
![\frac{1}{\Delta \mathbf{[z]}} \begin{bmatrix} z_{22} & -z_{12} \\ -z_{21} & z_{11} \end{bmatrix}](../I/m/a9a826c6447ba504d30b6b959b44bce8.png) |
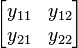 |
![\frac{1}{h_{11}} \begin{bmatrix} 1 & -h_{12} \\ h_{21} & \Delta \mathbf{[h]} \end{bmatrix}](../I/m/30118febb21dc17544d2817a4454049f.png) |
![\frac{1}{g_{22}} \begin{bmatrix} \Delta \mathbf{[g]} & g_{12} \\ -g_{21} & 1 \end{bmatrix}](../I/m/c9a0e42a7ef7846073a0d4b8e9d8dc3c.png) |
![\frac{1}{a_{12}} \begin{bmatrix} a_{22} & -\Delta \mathbf{[a]} \\ -1 & a_{11} \end{bmatrix}](../I/m/03af44a147b76995783d797e4dc67276.png) |
![\frac{1}{b_{12}} \begin{bmatrix} -b_{11} & 1 \\ \Delta \mathbf{[b]} & -b_{22} \end{bmatrix}](../I/m/303c702b7f3298c606e246e8e3f3622e.png) |
![\mathbf{[h]}](../I/m/dd88b463c4a0fd1740f49a6375ee2a42.png) |
![\frac{1}{z_{22}} \begin{bmatrix} \Delta \mathbf{[z]} & z_{12} \\ -z_{21} & 1 \end{bmatrix}](../I/m/fb1d625e1686c10d15c3fa096e2f7426.png) |
![\frac{1}{y_{11}} \begin{bmatrix} 1 & -y_{12} \\ y_{21} & \Delta \mathbf{[y]} \end{bmatrix}](../I/m/1c2bcf32a7e1a20a91b902c5277a3c90.png) |
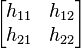 |
![\frac{1}{\Delta \mathbf{[g]}} \begin{bmatrix} g_{22} & -g_{12} \\ -g_{21} & g_{11} \end{bmatrix}](../I/m/1fd8c7d67712d60d5fec1f6ebbc9c915.png) |
![\frac{1}{a_{22}} \begin{bmatrix} a_{12} & \Delta \mathbf{[a]} \\ -1 & a_{21} \end{bmatrix}](../I/m/473acea6141de85eb0b8f357807f34d3.png) |
![\frac{1}{b_{11}} \begin{bmatrix} -b_{12} & 1 \\ -\Delta \mathbf{[b]} & -b_{21} \end{bmatrix}](../I/m/4d7a499a8230246d2a43551a0e0b771c.png) |
![\mathbf{[g]}](../I/m/a9566d52f3fe1ec530e00304f257b143.png) |
![\frac{1}{z_{11}} \begin{bmatrix} 1 & -z_{12} \\ z_{21} & \Delta \mathbf{[z]} \end{bmatrix}](../I/m/d5115f3b8a001f4a5f049fe987e746f0.png) |
![\frac{1}{y_{22}} \begin{bmatrix} \Delta \mathbf{[y]} & y_{12} \\ -y_{21} & 1 \end{bmatrix}](../I/m/72ab9bafd96ccb41a3b92b17bcf613b9.png) |
![\frac{1}{\Delta \mathbf{[h]}} \begin{bmatrix} h_{22} & -h_{12} \\ -h_{21} & h_{11} \end{bmatrix}](../I/m/a5c62620717b4c87950b1ba98bd84db5.png) |
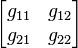 |
![\frac{1}{a_{11}} \begin{bmatrix} a_{21} & -\Delta \mathbf{[a]} \\ 1 & a_{12} \end{bmatrix}](../I/m/b41db331f4c8e2244b23bffa4f950f54.png) |
![\frac{1}{b_{22}} \begin{bmatrix} -b_{21} & -1 \\ \Delta \mathbf{[b]} & -b_{12} \end{bmatrix}](../I/m/28eaae65ce1637b32af846eb76a333aa.png) |
![\mathbf{[a]}](../I/m/46fb6e8076edcdfcc2bdc7bd547257b1.png) |
![\frac{1}{z_{21}} \begin{bmatrix} z_{11} & \Delta \mathbf{[z]} \\ 1 & z_{22} \end{bmatrix}](../I/m/11aca21368ea9cbf0d5bdf77a476668d.png) |
![\frac{1}{y_{21}} \begin{bmatrix} -y_{22} & -1 \\ -\Delta \mathbf{[y]} & -y_{11} \end{bmatrix}](../I/m/9ba874e720481aa36589f971b7ee306d.png) |
![\frac{1}{h_{21}} \begin{bmatrix} -\Delta \mathbf{[h]} & -h_{11} \\ -h_{22} & -1 \end{bmatrix}](../I/m/134f41a5333dd6693c55838dddceb1d4.png) |
![\frac{1}{g_{21}} \begin{bmatrix} 1 & g_{22} \\ g_{11} & \Delta \mathbf{[g]} \end{bmatrix}](../I/m/535c23e325e164a8ad50530bfb55f811.png) |
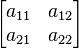 |
![\frac{1}{\Delta \mathbf{[b]}} \begin{bmatrix} b_{22} & -b_{12} \\ -b_{21} & b_{11} \end{bmatrix}](../I/m/b29fe2a24435a7ab17d844320d335293.png) |
![\mathbf{[b]}](../I/m/499e8b0761e9aa846009e894b6fd52d3.png) |
![\frac{1}{z_{12}} \begin{bmatrix} z_{22} & -\Delta \mathbf{[z]} \\ -1 & z_{11} \end{bmatrix}](../I/m/6af79b58298baa4c2754c2cbe9295426.png) |
![\frac{1}{y_{12}} \begin{bmatrix} -y_{11} & 1 \\ \Delta \mathbf{[y]} & -y_{22} \end{bmatrix}](../I/m/5025cbb7a28e2e8c08e3efbdad732c2b.png) |
![\frac{1}{h_{12}} \begin{bmatrix} 1 & -h_{11} \\ -h_{22} & \Delta \mathbf{[h]} \end{bmatrix}](../I/m/76fe95e9864517ba7281b23ba7f17d1c.png) |
![\frac{1}{g_{12}} \begin{bmatrix} -\Delta \mathbf{[g]} & g_{22} \\ g_{11} & -1 \end{bmatrix}](../I/m/d332ad7c57ded6afc80d6507c7a060ff.png) |
![\frac{1}{\Delta \mathbf{[a]}} \begin{bmatrix} a_{22} & -a_{12} \\ -a_{21} & a_{11} \end{bmatrix}](../I/m/8e3fde6c40892e9ba729cb972ed39cbb.png) |
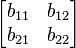 |
Where ![\Delta \mathbf{[x]}](../I/m/2ea141e65dd141da579529fd67e22455.png) is the determinant of [x].
is the determinant of [x].
Certain pairs of matrices have a particularly simple relationship. The admittance parameters are the matrix inverse of the impedance parameters, the inverse hybrid parameters are the matrix inverse of the hybrid parameters, and the [b] form of the ABCD-parameters is the matrix inverse of the [a] form. That is,
Networks with more than two ports
While two port networks are very common (e.g., amplifiers and filters), other electrical networks such as directional couplers and circulators have more than 2 ports. The following representations are also applicable to networks with an arbitrary number of ports:
For example three-port impedance parameters result in the following relationship:
However the following representations are necessarily limited to two-port devices:
- Hybrid (h) parameters
- Inverse hybrid (g) parameters
- Transmission (ABCD) parameters
- Scattering transfer (T) parameters
Collapsing a two-port to a one port
A two-port network has four variables with two of them being independent. If one of the ports is terminated by a load with no independent sources, then the load enforces a relationship between the voltage and current of that port. A degree of freedom is lost. The circuit now has only one independent parameter. The two-port becomes a one-port impedance to the remaining independent variable.
For example, consider impedance parameters
Connecting a load, ZL onto port 2 effectively adds the constraint
The negative sign is because the positive direction for I2 is directed into the two-port instead of into the load. The augmented equations become
The second equation can be easily solved for I2 as a function of I1 and that expression can replace I2 in the first equation leaving V1 ( and V2 and I2 ) as functions of I1
So, in effect, I1 sees an input impedance 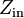 and the two-port's effect on the input circuit has been effectively collapsed down to a one-port; i.e., a simple two terminal impedance.
and the two-port's effect on the input circuit has been effectively collapsed down to a one-port; i.e., a simple two terminal impedance.
See also
Notes
- ↑ The emitter-leg resistors counteract any current increase by decreasing the transistor VBE. That is, the resistors RE cause negative feedback that opposes change in current. In particular, any change in output voltage results in less change in current than without this feedback, which means the output resistance of the mirror has increased.
- ↑ The double vertical bar denotes parallel connection of the resistors:
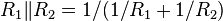 .
.
References
- ↑ Gray, §3.2, p. 172
- ↑ Jaeger, §10.5 §13.5 §13.8
- ↑ Jasper J. Goedbloed. "Reciprocity and EMC measurements" (PDF). EMCS. Retrieved 28 April 2014.
- ↑ Nahvi, p.311.
- ↑ Matthaei et al, pp. 70–72.
- 1 2 Matthaei et al, p.27.
- 1 2 Matthaei et al, p.29.
- ↑ Matthaei et al, p.26.
- ↑ Ghosh, p.353.
- ↑ Farago, p.102.
- ↑ Clayton, p.271.
- 1 2 Vasileska & Goodnick, p.137
- ↑ Egan, pp.11-12
- ↑ Carlin, p.304
- ↑ Matthaei et al, p.44.
- ↑ Egan, pp.12-15
- ↑ Egan, pp.13-14
- 1 2 Farago, pp.122-127.
- ↑ Ghosh, p.371.
- ↑ Farago, p.128.
- ↑ Ghosh, p.372.
- ↑ Ghosh, p.373.
- ↑ Farago, pp.128-134.
Bibliography
- Carlin, HJ, Civalleri, PP, Wideband circuit design, CRC Press, 1998. ISBN 0-8493-7897-4.
- William F. Egan, Practical RF system design, Wiley-IEEE, 2003 ISBN 0-471-20023-9.
- Farago, PS, An Introduction to Linear Network Analysis, The English Universities Press Ltd, 1961.
- Gray, P.R.; Hurst, P.J.; Lewis, S.H.; Meyer, R.G. (2001). Analysis and Design of Analog Integrated Circuits (4th ed.). New York: Wiley. ISBN 0-471-32168-0.
- Ghosh, Smarajit, Network Theory: Analysis and Synthesis, Prentice Hall of India ISBN 81-203-2638-5.
- Jaeger, R.C.; Blalock, T.N. (2006). Microelectronic Circuit Design (3rd ed.). Boston: McGraw–Hill. ISBN 978-0-07-319163-8.
- Matthaei, Young, Jones, Microwave Filters, Impedance-Matching Networks, and Coupling Structures, McGraw-Hill, 1964.
- Mahmood Nahvi, Joseph Edminister, Schaum's outline of theory and problems of electric circuits, McGraw-Hill Professional, 2002 ISBN 0-07-139307-2.
- Dragica Vasileska, Stephen Marshall Goodnick, Computational electronics, Morgan & Claypool Publishers, 2006 ISBN 1-59829-056-8.
- Clayton R. Paul, Analysis of Multiconductor Transmission Lines, John Wiley & Sons, 2008 ISBN 0470131543, 9780470131541.
|
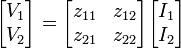
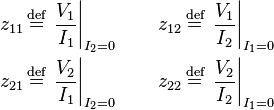
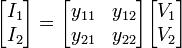
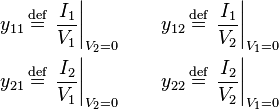
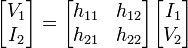
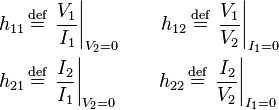
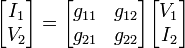
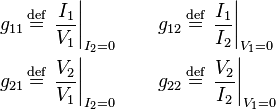
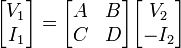
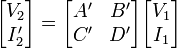
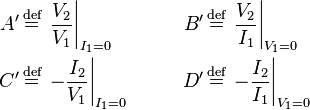
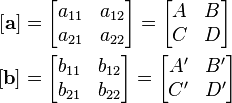
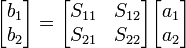
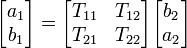
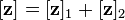
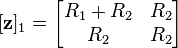
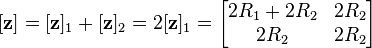
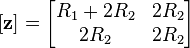
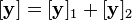
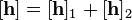
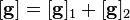
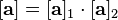
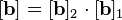
![\begin{align}[]
\left\lbrack\mathbf{b}\right\rbrack_1 &= \begin{bmatrix} 1 & -R \\ 0 & 1 \end{bmatrix}\\
\left\lbrack\mathbf{b}\right\rbrack_2 &= \begin{bmatrix} 1 & 0 \\ -sC & 1 \end{bmatrix}
\end{align}](../I/m/f0c69e6b190e9dc834b42a6aac544c75.png)
![\begin{align}[]
\lbrack\mathbf{b}\rbrack &= \lbrack\mathbf{b}\rbrack_2 \cdot \lbrack\mathbf{b}\rbrack_1 \\
&= \begin{bmatrix} 1 & 0 \\ -sC & 1 \end{bmatrix} \begin{bmatrix} 1 & -R \\ 0 & 1 \end{bmatrix} \\
&= \begin{bmatrix} 1 & -R \\ -sC & 1 + sCR \end{bmatrix}
\end{align}](../I/m/f4e0cde9c31b9a2c0ce59d7929cd6654.png)
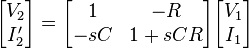
![\begin{align}
\left[\mathbf{y}\right] &= \left[\mathbf{z}\right]^{-1} \\
\left[\mathbf{g}\right] &= \left[\mathbf{h}\right]^{-1} \\
\left[\mathbf{b}\right] &= \left[\mathbf{a}\right]^{-1}
\end{align}](../I/m/3c2662ab5b72865a4c8f6e5f3772da24.png)