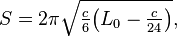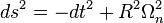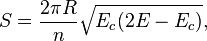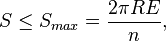Cardy formula

In physics, the Cardy formula is important because it gives the entropy of black holes. In recent years, this formula has appeared in not only the calculation of the entropy of BTZ black holes but also in checking the AdS/CFT correspondence and the holographic principle.

In 1986 J. L. Cardy discovered the following formula Cardy (1986), which gives the entropy of a (1+1)-dimensional conformal field theory (CFT):

S=2\pi\sqrt{\tfrac{c}{6}\bigl(L_0-\tfrac{c}{24}\bigr)},

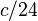Here $c$ is the central charge, $L_0 = ER$ is the product of the total energy and radius of the system, and the shift of $c/24$ is caused by the Casimir effect. $c$ and $L_0$ lie in the Virasoro algebra of this CFT. In 2000 E. Verlinde extended this formula to the arbitrary (n+1)-dimensions Verlinde (2000), so it is also called Cardy-Verlinde formula. Consider a AdS space with the metric

ds^2=-dt^2+R^2\Omega^2_n

where R is the radius of a n-dimensional sphere. The dual CFT lives on the boundary of this AdS space. The entropy of the dual CFT can be given by this formula as

S=\frac{2\pi R}{n}\sqrt{E_c(2E-E_c)},

where E_c is the Casimir effect, E total energy. The above reduced formula gives the maximal entropy

S\le S_{max}=\frac{2\pi RE}{n},

when E_c=E. This is just the Bekenstein bound. The Cardy-Verlinde formula was later shown by Kutasov and Larsen to be invalid for weakly interacting CFTs. In fact, since the entropy of higher dimensional (meaning n>1) CFTs is dependent on exactly marginal couplings, it is believed that a Cardy formula for the entropy is not achievable when n>1. However, for supersymmetric CFTs, a twisted version of the partition function, called "the superconformal index" (related to the Witten index) is shown by Di Pietro and Komargodski to exhibit Cardy-like behavior when n=3 or 5.

References

Cardy, John (1986), Operator content of two-dimensional conformal invariant theory, Nucl. Phys. B, 270 186
Carlip, Steven (2005), Conformal Field Theory, (2+1)-Dimensional Gravity, and the BTZ Black Hole, arXiv:gr-qc/0503022, Bibcode:2005CQGra..22R..85C, doi:10.1088/0264-9381/22/12/R01
Verlinde, Erik (2000). "On the Holographic Principle in a Radiation Dominated Universe". arXiv:hep-th/0008140.
D. Kutasov and F. Larsen (2000). "Partition Sums and Entropy Bounds in Weakly Coupled CFT". arXiv:hep-th/0009244.
L. Di Pietro, Z. Komargodski (2014). "Cardy Formulae for SUSY Theories in d=4 and d=6". arXiv:1407.6061.

This article is issued from Wikipedia - version of the Thursday, January 21, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Cardy formula

See also

References