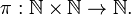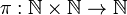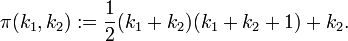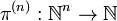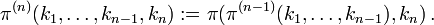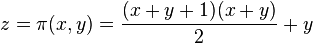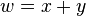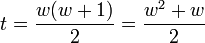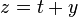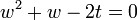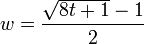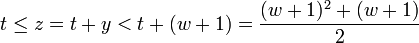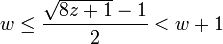Pairing function

In mathematics a pairing function is a process to uniquely encode two natural numbers into a single natural number.

Any pairing function can be used in set theory to prove that integers and rational numbers have the same cardinality as natural numbers. In theoretical computer science they are used to encode a function defined on a vector of natural numbers f:N^k → N into a new function g:N → N.

Definition

A pairing function is a primitive recursive bijection

\pi:\mathbb{N} \times \mathbb{N} \to \mathbb{N}.

Cantor pairing function

The Cantor pairing function assigns one natural number to each pair of natural numbers

The Cantor pairing function is a pairing function

\pi:\mathbb{N} \times \mathbb{N} \to \mathbb{N}

defined by

\pi(k_1,k_2) := \frac{1}{2}(k_1 + k_2)(k_1 + k_2 + 1)+k_2.

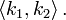
The statement that this is the only quadratic pairing function is known as the Fueter–Pólya theorem. Whether this is the only polynomial pairing function is still an open question. When we apply the pairing function to $k_1$ and $k_2$ we often denote the resulting number as $\langle k_1, k_2 \rangle \,.$

This definition can be inductively generalized to the Cantor tuple function

\pi^{(n)}:\mathbb{N}^n \to \mathbb{N}

\pi^{(n)}(k_1, \ldots, k_{n-1}, k_n) := \pi ( \pi^{(n-1)}(k_1, \ldots, k_{n-1}) , k_n) \,.

Inverting the Cantor pairing function

Let 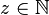$z \in \mathbb{N}$ be arbitrary and suppose that 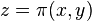$z = \pi(x, y)$ . We will show that there exist unique values 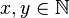$x, y \in \mathbb{N}$ such that

z = \pi(x, y) = \frac{(x + y + 1)(x + y)}{2} + y

and hence that 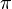$\pi$ is invertible. It is helpful to define some intermediate values in the calculation:

w = x + y \!

t = \frac{w(w + 1)}{2} = \frac{w^2 + w}{2}

z = t + y \!

where t is the triangle number of w. If we solve the quadratic equation

w^2 + w - 2t = 0 \!

for w as a function of t, we get

w = \frac{\sqrt{8t + 1} - 1}{2}

which is a strictly increasing and continuous function when t is non-negative real. Since

t \leq z = t + y < t + (w + 1) = \frac{(w + 1)^2 + (w + 1)}{2}

we get that

w \leq \frac{\sqrt{8z + 1} - 1}{2} < w + 1

and thus

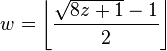w = \left\lfloor \frac{\sqrt{8z + 1} - 1}{2} \right\rfloor

where $\left\lfloor \, \right\rfloor$ is the floor function. So to calculate x and y from z, we do:

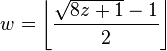
w = \left\lfloor \frac{\sqrt{8z + 1} - 1}{2} \right\rfloor

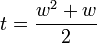
t = \frac{w^2 + w}{2}

y = z - t \!

x = w - y \!

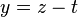
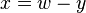Since the Cantor pairing function is invertible, it must be one-to-one and onto.

Examples

To calculate π (47, 32):

47+32 = 79
79+1 = 80
79×80 = 6320
6320÷2 = 3160
3160+32 = 3192

so π (47, 32) = 3192.

To find x and y such that π (x, y) = 1432:

8×1432 = 11456
11456+1 = 11457
√11457 = 107.037
107.037-1 = 106.037
106.037÷2 = 53.019
⌊53.019⌋ = 53

so w = 53

53+1 = 54
53×54 = 2862
2862÷2 = 1431

so t = 1431

1432-1431 = 1

so y = 1

53-1 = 52

so x = 52; thus π (52, 1) = 1432.

References

Steven Pigeon, "Pairing function", MathWorld.

External links

An Elegant Pairing Function

This article is issued from Wikipedia - version of the Monday, December 21, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.