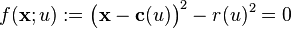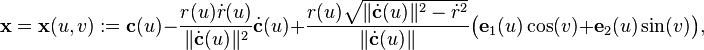Channel surface

canalsurface: directrix is a helix, with its generating spheres

pipe surface: directrix is a helix, with generating spheres

pipe surface: directrix is a helix

A channel or canal surface is a surface formed as the envelope of a family of spheres whose centers lie on a space curve, its directrix. If the radii of the generating spheres are constant the canal surface is called pipe surface. Simple examples are:

right circular cylinder (pipe surface, directrix is a line, the axis of the cylinder)
torus (pipe surface, directrix is a circle),
right circular cone (canal surface, directrix is a line (the axis), radii of the spheres not constant),
surface of revolution (canal surface, directrix is a line),

Canal surfaces play an essential role in descriptive geometry, because in case of an orthographic projection its contour curve can be drawn as the envelope of circles.

In technical area canal surfaces can be used for blending surfaces smoothly.

Envelope of a pencil of implicit surfaces

Given the pencil of implicit surfaces

\Phi_c: f({\mathbf x},c)=0 , c\in [c_1,c_2]

Two neighboring surfaces 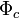$\Phi_c$ and $\Phi_{c+\Delta c}$ intersect in a curve that fulfills the equations

f({\mathbf x},c)=0

and

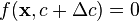f({\mathbf x},c+\Delta c)=0

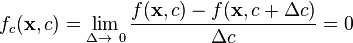For the limit $\Delta c \to 0$ one gets $f_c({\mathbf x},c)= \lim_{\Delta \to \ 0} \frac{f({\mathbf x},c)-f({\mathbf x},c+\Delta c)}{\Delta c}=0$ . The last equation is the reason for the following definition

Let be $\Phi_c: f({\mathbf x},c)=0 , c\in [c_1,c_2]$ a 1-parameter pencil of regular implicit $C^2$ - surfaces ( $f$ is at least twice continuously differentiable). The surface defined by the two equations
$f({\mathbf x},c)=0, \quad f_c({\mathbf x},c)=0$

is the envelope of the given pencil of surfaces.^[1]

Canal surface

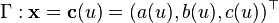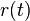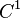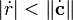Let be $\Gamma: {\mathbf x}={\mathbf c}(u)=(a(u),b(u),c(u))^\top$ a regular space curve and $r(t)$ a $C^1$ -function with $r>0$ and $|\dot{r}|<\|\dot{\mathbf c}\|$ . The last condition means that the curvature of the curve is less than that of the corresponding sphere.

The envelope of the 1-parameter pencil of spheres

f({\mathbf x};u):= \big({\mathbf x}-{\mathbf c}(u)\big)^2-r(u)^2=0

is called canal surface and 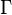$\Gamma$ its directrix. If the radii are constant, it is called pipe surface.

Parametric representation of a canal surface

The envelope condition

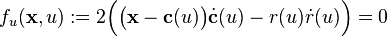f_u({\mathbf x},u):= 2\Big(\big({\mathbf x}-{\mathbf c}(u)\big)\dot{\mathbf c}(u)-r(u)\dot{r}(u)\Big)=0

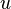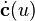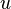of the canal surface above is for any value of $u$ the equation of a plane, which is orthogonal to the tangent $\dot{\mathbf c}(u)$ of the directrix . Hence the envelope is a collection of circles. This property is the key for a parametric representation of the canal surface. The center of the circle (for parameter $u$ ) has the distance $d:=\frac{r\dot{r}}{\|\dot{\mathbf c}\|}<r$ (s. 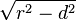condition above) from the center of the corresponding sphere and its radius is $\sqrt{r^2-d^2}$ . Hence

${\mathbf x}={\mathbf x}(u,v):= {\mathbf c}(u)-\frac{r(u)\dot{r}(u)}{\|\dot{\mathbf c}(u)\|^2}\dot{\mathbf c}(u) +\frac{r(u)\sqrt{\|\dot{\mathbf c}(u)\|^2-\dot{r}^2}}{\|\dot{\mathbf c}(u)\|} \big({\mathbf e}_1(u)\cos(v)+ {\mathbf e}_2(u)\sin(v)\big),$

where the vectors 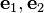${\mathbf e}_1,{\mathbf e}_2$ and the tangenten vector 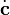$\dot{\mathbf c}$ form a orthonormal basis, is a parametric representation of the canal surface.^[2]

For 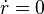$\dot{r}=0$ one gets the parametric representation of a pipe surface:

${\mathbf x}={\mathbf x}(u,v):= {\mathbf c}(u)+r\big({\mathbf e}_1(u)\cos(v)+ {\mathbf e}_2(u)\sin(v)\big).$

pipe knot

canal surface: Dupin cyclide

Examples

a) The first picture shows a canal surface with

the helix $(\cos(u),\sin(u), 0.25u), u\in[0,4]$ as directrix and
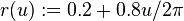the radius function $r(u):= 0.2+0.8u/2\pi$ .
The choice for 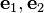${\mathbf e}_1,{\mathbf e}_2$ is the following:

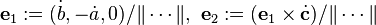{\mathbf e}_1:=(\dot{b},-\dot{a},0)/\|\cdots\|,\ {\mathbf e}_2:= ({\mathbf e}_1\times \dot{\mathbf c})/\|\cdots\|

b) For the second picture the radius is constant:

r(u):= 0.2

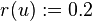, i. e. the canal surface is a pipe surface.

c) For the 3. picture the pipe surface b) has parameter

u\in[0,7.5]

d) The 4. picture shows a pipe knot. Its directrix is a curve on a torus

e) The 5. picture shows a Dupin cyclide (canal surface).

References

Hilbert, David; Cohn-Vossen, Stephan (1952). Geometry and the Imagination (2nd ed.). Chelsea. p. 219. ISBN 0-8284-1087-9.

External links

M. Peternell and H. Pottmann: Computing Rational Parametrizations of Canal Surfaces

This article is issued from Wikipedia - version of the Thursday, January 07, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.