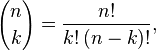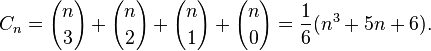Cake number

In mathematics, the cake number, denoted by Cn, is the maximum number of regions into which a 3-dimensional cube can be partitioned by exactly n planes. The cake number is so-called because one may imagine each partition of the cube by a plane as a slice made by a knife through a cube-shaped cake.

The values of Cn for increasing n ≥ 0 are given by 1, 2, 4, 8, 15, 26, 42, 64, 93, …(sequence A000125 in OEIS)

The cake numbers are the 3-dimensional analogue of the 2-dimensional lazy caterer's sequence; the difference between successive cake numbers also gives the lazy caterer's sequence.

Animation showing the cutting planes required to cut a cake into 15 pieces with 4 cutting planes (representing the 5th cake number). Fourteen of the pieces would have an external surface, with one tetrahedron cut out of the middle.

General formula

If n! denotes the factorial, and we denote the binomial coefficients by

{n \choose k} = \frac{n!}{k! \, (n-k)!} ,

and we assume that n planes are available to partition the cube, then the number is:[1]

C_n = {n \choose 3} + {n \choose 2} + {n \choose 1} + {n \choose 0} = \frac{1}{6}(n^3 + 5n + 6).

References

  1. ↑ Eric Weisstein. "Space Division by Planes". MathWorld − A Wolfram Web Resource. Retrieved August 19, 2010.


This article is issued from Wikipedia - version of the Saturday, July 25, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.