Carl Gustav Jacob Jacobi
| Carl Gustav Jacob Jacobi | |
|---|---|
 | |
| Born |
10 December 1804 Potsdam, Kingdom of Prussia |
| Died |
18 February 1851 (aged 46) Berlin, Kingdom of Prussia |
| Residence | Prussia |
| Nationality | German |
| Fields | Mathematician |
| Institutions | Königsberg University |
| Alma mater | University of Berlin |
| Thesis | Disquisitiones Analyticae de Fractionibus Simplicibus (1825) |
| Doctoral advisor | Enno Dirksen |
| Doctoral students |
Paul Gordan Otto Hesse Friedrich Julius Richelot |
| Known for |
Jacobi's elliptic functions Jacobian Jacobi symbol Jacobi identity Jacobi operator Hamilton–Jacobi equation |
Carl Gustav Jacob Jacobi (/dʒəˈkoʊbi/;[1] German: [jaˈkoːbi]; 10 December 1804 – 18 February 1851) was a German mathematician, who made fundamental contributions to elliptic functions, dynamics, differential equations, and number theory. His name is occasionally written as Carolus Gustavus Iacobus Iacobi in his Latin books, and his first name is sometimes given as Karl.
Jacobi was the first Jewish mathematician to be appointed professor at a German university.[2]
Biography
Jacobi was born of Ashkenazi Jewish parentage in Potsdam on 10 December 1804. He was the second of the four children of banker Simon Jacobi, out of which his elder brother Moritz von Jacobi would also become known later as an engineer and physicist. He was initially home schooled by his uncle Lehman, who instructed him in the classical languages and elements of mathematics. In 1816, the twelve-year-old Jacobi went to the Potsdam Gymnasium, where students were being taught classical languages, German history as well as mathematics. As a result of the good education received from his uncle, as well as his own remarkable abilities, after less than half a year Jacobi was moved to the senior year despite his young age. However, as the University was not accepting students younger than 16 years old, he had to remain in the senior class until 1821. He used this time to advance his knowledge, showing interest in all subjects, including Latin and Greek, philology, history and mathematics. During this period he also made the first attempts at research trying to solve the quintic equation by radicals.[3]
In 1821 Jacobi went to study at the Berlin University, where initially he divided his attention between his passions for philology and mathematics. In philology he participated in the seminars of Böckh, drawing the professor's attention with his talent. Jacobi did not follow a lot of mathematics classes at the University, as the low level of mathematics in Germany at the time rendered them too elementary for him. However, he continued with his private study of the more advanced works of Euler, Lagrange and Laplace. By 1823 he understood that he needed to make a decision between his competing interests and he chose to devote all his attention to mathematics.[4] In the same year he became qualified to teach secondary school and was offered a position at the Joachimsthal Gymnasium in Berlin. Jacobi decided instead to continue to work towards a University position. In 1825 he obtained the degree of Doctor of Philosophy with a dissertation on the partial fraction decomposition of rational fractions defended before a commission led by Enno Dirksen. He followed immediately with his Habilitation and at the same time converted to Christianity. Now qualifying for teaching University classes, the 21-year-old Jacobi lectured in 1825/26 on the theory of curves and surfaces at the University of Berlin.[4][5]
In 1827 he became a professor and in 1829, a tenured professor of mathematics at Königsberg University, and held the chair until 1842.
Jacobi suffered a breakdown from overwork in 1843. He then visited Italy for a few months to regain his health. On his return he moved to Berlin, where he lived as a royal pensioner until his death. During the Revolution of 1848 Jacobi was politically involved and unsuccessfully presented his parliamentary candidature on behalf of a Liberal club. This led, after the suppression of the revolution, to his royal grant being cut off – but his fame and reputation were such that it was soon resumed. In 1836, he had been elected a foreign member of the Royal Swedish Academy of Sciences.
Jacobi died in 1851 from a smallpox infection. His grave is preserved at a cemetery in the Kreuzberg section of Berlin, the Friedhof I der Dreifaltigkeits-Kirchengemeinde (61 Baruther Street). His grave is close to that of Johann Encke, the astronomer. The crater Jacobi on the Moon is named after him.
Scientific contributions
One of Jacobi's greatest accomplishments was his theory of elliptic functions and their relation to the elliptic theta function. This was developed in his great treatise Fundamenta nova theoriae functionum ellipticarum (1829), and in later papers in Crelle's Journal. Theta functions are of great importance in mathematical physics because of their role in the inverse problem for periodic and quasi-periodic flows. The equations of motion are integrable in terms of Jacobi's elliptic functions in the well-known cases of the pendulum, the Euler top, the symmetric Lagrange top in a gravitational field and the Kepler problem (planetary motion in a central gravitational field).
He also made fundamental contributions in the study of differential equations and to rational mechanics, notably the Hamilton–Jacobi theory.
It was in algebraic development that Jacobi’s peculiar power mainly lay, and he made important contributions of this kind to many areas of mathematics, as shown by his long list of papers in Crelle’s Journal and elsewhere from 1826 onwards. One of his maxims was: 'Invert, always invert' ('man muss immer umkehren'), expressing his belief that the solution of many hard problems can be clarified by re-expressing them in inverse form.
In his 1835 paper, Jacobi proved the following basic result classifying periodic (including elliptic) functions: If a univariate single-valued function is multiply periodic, then such a function cannot have more than two periods, and the ratio of the periods cannot be a real number. He discovered many of the fundamental properties of theta functions, including the functional equation and the Jacobi triple product formula, as well as many other results on q-series and hypergeometric series.
The solution of the Jacobi inversion problem for the hyperelliptic Abel map by Weierstrass in 1854 required the introduction of the hyperelliptic theta function and later the general Riemann theta function for algebraic curves of arbitrary genus. The complex torus associated to a genus  algebraic curve, obtained by quotienting
algebraic curve, obtained by quotienting 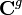 by the lattice of periods is referred to as the Jacobian variety. This method of inversion, and its subsequent extension by Weierstrass and Riemann to arbitrary algebraic curves, may be seen as a higher genus generalization of the relation between elliptic integrals and the Jacobi, or Weierstrass elliptic functions
by the lattice of periods is referred to as the Jacobian variety. This method of inversion, and its subsequent extension by Weierstrass and Riemann to arbitrary algebraic curves, may be seen as a higher genus generalization of the relation between elliptic integrals and the Jacobi, or Weierstrass elliptic functions

Jacobi was the first to apply elliptic functions to number theory, for example proving of Fermat's two-square theorem and Lagrange's four-square theorem, and similar results for 6 and 8 squares. His other work in number theory continued the work of C. F. Gauss: new proofs of quadratic reciprocity and introduction of the Jacobi symbol; contributions to higher reciprocity laws, investigations of continued fractions, and the invention of Jacobi sums.
He was also one of the early founders of the theory of determinants; in particular, he invented the Jacobian determinant formed from the n² differential coefficients of n given functions of n independent variables, and which has played an important part in many analytical investigations. In 1841 he reintroduced the partial derivative ∂ notation of Legendre, which was to become standard.
Students of vector fields and Lie theory often encounter the Jacobi identity, the analog of associativity for the Lie bracket operation.
Planetary theory and other particular dynamical problems likewise occupied his attention from time to time. While contributing to celestial mechanics, he introduced the Jacobi integral (1836) for a sidereal coordinate system. His theory of the last multiplier is treated in Vorlesungen über Dynamik, edited by Alfred Clebsch (1866).
He left many manuscripts, portions of which have been published at intervals in Crelle's Journal. His other works include Commentatio de transformatione integralis duplicis indefiniti in formam simpliciorem (1832), Canon arithmeticus (1839), and Opuscula mathematica (1846–1857). His Gesammelte Werke (1881–1891) were published by the Berlin Academy.
Publications
- Jacobi, C. G. J. (1829), Fundamenta nova theoriae functionum ellipticarum (in Latin), Königsberg, ISBN 978-1-108-05200-9, Reprinted by Cambridge University Press 2012
- Jacobi, C. G. J. (1969) [1881], Gesammelte Werke, Herausgegeben auf Veranlassung der Königlich Preussischen Akademie der Wissenschaften, I-VIII (2nd ed.), New York: Chelsea Publishing Co., MR 0260557
- Jacobi, Carl Gustav Jacob (1839), Canon arithmeticus, sive tabulae quibus exhibentur pro singulis numeris primis vel primorum potestatibus infra 1000 numeri ad datos indices et indices ad datos numeros pertinentes, Berlin: Typis Academicis, Berolini, MR 0081559
- Jacobi, Carl Gustav Jacob (1996) [1848], Vorlesungen über analytische Mechanik, Dokumente zur Geschichte der Mathematik [Documents on the History of Mathematics] 8, Freiburg: Deutsche Mathematiker Vereinigung, doi:10.1007/978-3-322-80289-7, ISBN 978-3-528-06692-5, MR 1414679
- Jacobi, Carl Gustav Jacob (2007) [1836], Vorlesungen über Zahlentheorie---Wintersemester 1836/37, Königsberg, Algorismus. Studien zur Geschichte der Mathematik und der Naturwissenschaften [Algorismus. Studies in the History of Mathematics and the Natural Sciences] 62, Dr. Erwin Rauner Verlag, Augsburg, ISBN 978-3-936905-25-0, MR 2573816
- Jacobi, Carl Gustav Jacob (2009) [1866], Clebsch, A.; Balagangadharan, K.; Banerjee, Biswarup, eds., Jacobi's lectures on dynamics, Texts and Readings in Mathematics 51, New Delhi: Hindustan Book Agency, ISBN 9788185931913, MR 2569315
- Jacobi, Carl Gustav Jacob (2009) [1866], Ollivier, François; Cohn, Sigismund; Borchardt, C. W.; et al., eds., "The reduction to normal form of a non-normal system of differential equations", Applicable Algebra in Engineering, Communication and Computing, Translation of De aequationum differentialium systemate non normali ad formam normalem revocando 20 (1): 33–64, doi:10.1007/s00200-009-0088-2, ISSN 0938-1279, MR 2496660
- Jacobi, Carl Gustav Jacob (2009) [1865], Ollivier, François; Cohn, Sigismund; Borchardt., C. W., eds., "Looking for the order of a system of arbitrary ordinary differential equations", Applicable Algebra in Engineering, Communication and Computing, Translation of De investigando ordine systematis æquationibus differentialium vulgarium cujuscunque 20 (1): 7–32, doi:10.1007/s00200-009-0087-3, ISSN 0938-1279, MR 2496659
See also
- List of things named after Carl Gustav Jacob Jacobi
- Friedrich Wilhelm August Argelander
- Augustin-Louis Cauchy
- Johann Friedrich Herbart
- Friedrich Wilhelm Bessel
Notes
- ↑ "Jacobi, Carl Gustav Jacob". Random House Webster's Unabridged Dictionary.
- ↑ Setting the record straight about Jewish mathematicians in Nazi Germany, Haaretz
- ↑ Koenigsberger, Leo (1904), Carl Gustav Jacob Jacobi, Festschrift zur Feier der hundertsten Wiederkehr seines Geburtstages (in German), Leipzig, B.G. Teubner, Review by Pierpont
- 1 2 Dirichlet, P. G. Lejeune (1855), "Gedächtnißrede auf Carl Gustav Jacob Jacobi", Journal für die reine und angewandte Mathematik 52: 193–217, ISSN 0075-4102, MR 1104895
- ↑ James, Ioan Mackenzie (2003). Remarkable Mathematicians: From Euler to von Neumann. Cambridge University Press. pp. 69–74. ISBN 978-0-521-52094-2.
References
- Temple Bell, Eric (1937). Men of Mathematics. New York: Simon and Schuster.
- Moritz Cantor (1905), "Jacobi, Carl Gustav Jacob", Allgemeine Deutsche Biographie (ADB) (in German) 50, Leipzig: Duncker & Humblot, pp. 598–602
- Dirichlet, P. G. Lejeune (1855), "Gedächtnißrede auf Carl Gustav Jacob Jacobi", Journal für die reine und angewandte Mathematik 52: 193–217, ISSN 0075-4102, MR 1104895
 This article incorporates text from a publication now in the public domain: Chisholm, Hugh, ed. (1911). "Jacobi, Karl Gustav Jacob". Encyclopædia Britannica (11th ed.). Cambridge University Press.
This article incorporates text from a publication now in the public domain: Chisholm, Hugh, ed. (1911). "Jacobi, Karl Gustav Jacob". Encyclopædia Britannica (11th ed.). Cambridge University Press.- Koenigsberger, Leo (1904), Carl Gustav Jacob Jacobi, Festschrift zur Feier der hundertsten Wiederkehr seines Geburtstages (in German), Leipzig, B.G. Teubner, Review by Pierpont
- Christoph J. Scriba (1974), "Jacobi, Carl Gustav Jacob", Neue Deutsche Biographie (NDB) (in German) 10, Berlin: Duncker & Humblot, pp. 233–234; (full text online)
External links
| Wikiquote has quotations related to: Carl Gustav Jacob Jacobi |
- Jacobi's Vorlesungen über Dynamik
- O'Connor, John J.; Robertson, Edmund F., "Carl Gustav Jacob Jacobi", MacTutor History of Mathematics archive, University of St Andrews.
-
 "Jacobi, Karl Gustav Jakob". Encyclopedia Americana. 1920.
"Jacobi, Karl Gustav Jakob". Encyclopedia Americana. 1920. -
 "Jacobi, Karl Gustav Jakob". New International Encyclopedia. 1905.
"Jacobi, Karl Gustav Jakob". New International Encyclopedia. 1905. -
 "Jacobi, Karl Gustav Jakob". The American Cyclopædia. 1879.
"Jacobi, Karl Gustav Jakob". The American Cyclopædia. 1879.
- Carl Gustav Jacob Jacobi - Œuvres complètes Gallica-Math
|