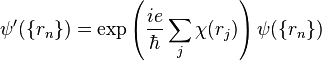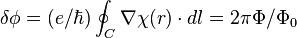Byers-Yang theorem

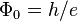In quantum mechanics, the Byers-Yang theorem states that all physical properties of a doubly connected system (an annulus) enclosing a magnetic flux $\Phi$ through the opening are periodic in the flux with period $\Phi_0=h/e$ (the magnetic flux quantum). The theorem was first stated and proven by Nina Byers and Chen-Ning Yang (1961),^[1] and further developed by Felix Bloch (1970).^[2]

Proof

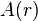An enclosed flux $\Phi$ corresponds to a vector potential $A(r)$ inside the annulus with a line integral 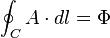$\oint_C A\cdot dl=\Phi$ along any path 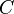$C$ that circulates around once. One can try to eliminate this vector potential by the gauge transformation

\psi'(\{r_n\})=\exp\left(\frac{ie}{\hbar}\sum_j\chi(r_j)\right)\psi(\{r_n\})

of the wave function 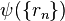$\psi(\{r_n\})$ of electrons at positions 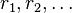$r_1,r_2,\ldots$ . The gauge-transformed wave function satisfies the same Schrödinger equation as the original wave function, but with a different magnetic vector potential 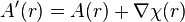$A'(r)=A(r)+\nabla\chi(r)$ . It is assumed that the electrons experience zero magnetic field 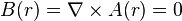$B(r)=\nabla\times A(r)=0$ at all points $r$ inside the annulus, the field being nonzero only within the opening (where there are no electrons). 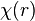It is then always possible to find a function $\chi(r)$ such that 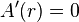$A'(r)=0$ inside the annulus, so one would conclude that the system with enclosed flux $\Phi$ is equivalent to a system with zero enclosed flux.

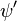However, for any arbitrary $\Phi$ the gauge transformed wave function is no longer single-valued: The phase of $\psi'$ changes by

\delta\phi=(e/\hbar)\oint_C\nabla\chi(r)\cdot dl=2\pi\Phi/\Phi_0

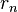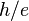whenever one of the coordinates $r_n$ is moved along the ring to its starting point. The requirement of a single-valued wave function therefore restricts the gauge transformation to fluxes $\Phi$ that are an integer multiple of $\Phi_0$ . Systems that enclose a flux differing by a multiple of $h/e$ are equivalent.

Applications

An overview of physical effects governed by the Byers-Yang theorem is given by Yoseph Imry.^[3] These include the Aharonov-Bohm effect, persistent current in normal metals, and flux quantization in superconductors.

Notes

↑ Byers, N.; Yang, C. (1961). "Theoretical Considerations Concerning Quantized Magnetic Flux in Superconducting Cylinders". Physical Review Letters 7 (2): 46–49. doi:10.1103/PhysRevLett.7.46.
↑ Bloch, F. (1970). "Josephson Effect in a Superconducting Ring". Physical Review B 2: 109–121. doi:10.1103/PhysRevB.2.109.
↑ Imry, Y. (1997). Introduction to Mesoscopic Physics. Oxford University Press. ISBN 0-19-510167-7.

This article is issued from Wikipedia - version of the Wednesday, September 30, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.