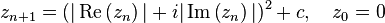Burning Ship fractal

High-quality overview image of the Burning Ship fractal

High-quality image of the large ship in the left antenna
The Burning Ship fractal, first described and created by Michael Michelitsch and Otto E. Rössler in 1992, is generated by iterating the function:
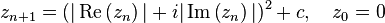
in the complex plane 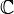 which will either escape or remain bounded. The difference between this calculation and that for the Mandelbrot set is that the real and imaginary components are set to their respective absolute values before squaring at each iteration. The mapping is non-analytic because its real and imaginary parts do not obey the Cauchy–Riemann equations.[1]
which will either escape or remain bounded. The difference between this calculation and that for the Mandelbrot set is that the real and imaginary components are set to their respective absolute values before squaring at each iteration. The mapping is non-analytic because its real and imaginary parts do not obey the Cauchy–Riemann equations.[1]
| Burning Ship fractal renderings |
|---|
| High-quality deep-zoom image of a small ship in the armada in the left Western antenna of the main ship structure |
| Burning Ship deep zoom to 2.3·10−50 |
| A zoom-in to the lower left of the Burning Ship fractal, showing a "burning ship" and self-similarity to the complete fractal |
| A zoom-in to line on the left of the fractal, showing nested repetition (a different colour scheme is used here) |
| High-quality image of the Burning Ship fractal |
| The Burning Ship fractal featured in the 1K intro "JenterErForetrukket" by Youth Uprising; a demoscene production |
| A corresponding Julia set of Burning Ship fractal |
| A corresponding Julia set of Burning Ship fractal |
|
References
- ↑ Michael Michelitsch and Otto E. Rössler (1992). "The "Burning Ship" and Its Quasi-Julia Sets". In: Computers & Graphics Vol. 16, No. 4, pp. 435–438, 1992. Reprinted in Clifford A. Pickover Ed. (1998). Chaos and Fractals: A Computer Graphical Journey — A 10 Year Compilation of Advanced Research. Amsterdam, Netherlands: Elsevier. ISBN 0-444-50002-2
External links


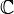 which will either escape or remain bounded. The difference between this calculation and that for the Mandelbrot set is that the real and imaginary components are set to their respective absolute values before squaring at each iteration. The mapping is non-analytic because its real and imaginary parts do not obey the Cauchy–Riemann equations.[1]
which will either escape or remain bounded. The difference between this calculation and that for the Mandelbrot set is that the real and imaginary components are set to their respective absolute values before squaring at each iteration. The mapping is non-analytic because its real and imaginary parts do not obey the Cauchy–Riemann equations.[1]