Brownian web
In probability theory, the Brownian web is an uncountable collection of one-dimensional coalescing Brownian motions, starting from every point in space and time. It arises as the diffusive space-time scaling limit of a collection of coalescing random walks, with one walk starting from each point of the integer lattice Z at each time.
History and Basic Description
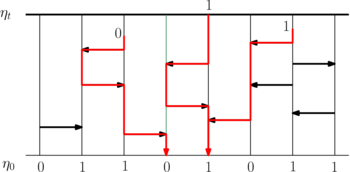
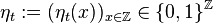 . The arrows determine when a voter changes its opinion to that of the neighbor pointed to by the arrow. The genealogies are obtained by following the arrows backwards in time, which are distributed as coalescing random walks.
. The arrows determine when a voter changes its opinion to that of the neighbor pointed to by the arrow. The genealogies are obtained by following the arrows backwards in time, which are distributed as coalescing random walks.What is now known as the Brownian web was first conceived by Arratia in his Ph.D. thesis [1] and a subsequent incomplete and unpublished manuscript.[2] Arratia studied the voter model, an interacting particle system that models the evolution of a population's political opinions. The individuals of the population are represented by the vertices of a graph, and each individual carries one of two possible opinions, represented as either 0 or 1. Independently at rate 1, each individual changes its opinion to that of a randomly chosen neighbor. The voter model is known to be dual to coalescing random walks (i.e., the random walks move independently when they are apart, and move as a single walk once they meet) in the sense that: each individual's opinion at any time can be traced backwards in time to an ancestor at time 0, and the joint genealogies of the opinions of different individuals at different times is a collection of coalescing random walks evolving backwards in time. In spatial dimension 1, coalescing random walks starting from a finite number of space-time points converge to a finite number of coalescing Brownian motions, if space-time is rescaled diffusively (i.e., each space-time point (x,t) gets mapped to (εx,ε^2t), with ε↓0). This is a consequence of Donsker's invariance principle. The less obvious question is:
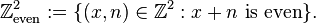 From each lattice point, an arrow is drawn either up-right or up-left with probability 1/2 each. The random walks move upward in time by following the arrows, and different random walks coalesce once they meet.
From each lattice point, an arrow is drawn either up-right or up-left with probability 1/2 each. The random walks move upward in time by following the arrows, and different random walks coalesce once they meet.What is the diffusive scaling limit of the joint collection of one-dimensional coalescing random walks starting from every point in space-time?
Arratia set out to construct this limit, which is what we now call the Brownian web. Formally speaking, it is a collection of one-dimensional coalescing Brownian motions starting from every space-time point in 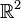 . The fact that the Brownian web consists of an uncountable number of Brownian motions is what makes the construction highly non-trivial.
. The fact that the Brownian web consists of an uncountable number of Brownian motions is what makes the construction highly non-trivial.
The complete construction of the Brownian web was carried out later by Tóth and Werner in their study of the true self-repelling motion.[3] The name Brownian web was coined by Fontes, Isopi, Newman and Ravishankar,[4] where they introduced a topology for the Brownian web so that it is realized as a random variable taking values in a Polish space, in this case, the space of compact sets of paths. The introduction of this topology allows one to formalize mathematically the convergence of the coalescing random walks to the Brownian web.
An extension of the Brownian web, called the Brownian net, has been introduced by Sun and Swart [5] by allowing the coalescing Brownian motions to undergo branching. An alternative construction of the Brownian net was given by Newman, Ravishankar and Schertzer.[6]
For a recent survey, see Schertzer, Sun and Swart.[7]
References
- ↑ Arratia, Richard Alejandro (1979-01-01). Coalescing Brownian Motions on the Line. University of Wisconsin--Madison.
- ↑ Arratia, Richard (1981). "Coalescing Brownian motions on $R$ and the voter model on $Z$.". Uncompleted manuscript.
- ↑ Tóth, Bálint; Werner, Wendelin (1998-07-01). "The true self-repelling motion". Probability Theory and Related Fields 111 (3): 375–452. doi:10.1007/s004400050172. ISSN 0178-8051.
- ↑ Fontes, L. R. G.; Isopi, M.; Newman, C. M.; Ravishankar, K. (2004-10-01). "The Brownian web: Characterization and convergence". The Annals of Probability 32 (4): 2857–2883. doi:10.1214/009117904000000568. ISSN 0091-1798.
- ↑ Sun, Rongfeng; Swart, Jan M. (2008-05-01). "The Brownian net". The Annals of Probability 36 (3): 1153–1208. doi:10.1214/07-AOP357. ISSN 0091-1798.
- ↑ Newman, C. M.; Ravishankar, K.; Schertzer, E. (2010-05-01). "Marking (1, 2) points of the Brownian web and applications". Annales de l'Institut Henri Poincaré, Probabilités et Statistiques 46 (2): 537–574. doi:10.1214/09-AIHP325. ISSN 0246-0203.
- ↑ Schertzer, Emmanuel; Sun, Rongfeng; Swart, Jan M. (2015-06-01). "The Brownian web, the Brownian net, and their universality". arXiv:1506.00724.