Broken diagonal
In recreational mathematics and the theory of magic squares, a broken diagonal is a set of n cells forming two parallel diagonal lines in the square. Alternatively, these two lines can be thought of as wrapping around the boundaries of the square to form a single sequence. A magic square in which the broken diagonals have the same sum as the rows, columns, and diagonals is called a panmagic square.[1][2]
Examples of broken diagonals from the below square are as follows: 3,12,14,5; 10,1,7,16; 10,13,7,4; 15,8,2,9; 15,12,2,5; and 6,13,11,4.

Notice that because one of the properties of a panmagic square is that the broken diagonals add up to the same constant, the following pattern is evident:
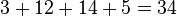 ;
;
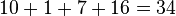 ;
;

One way to visualize a broken diagonal is to imagine a "ghost image" of the panmagic square adjacent to the original:


It is easy to see now how the set of numbers {3, 12, 14, 5} result to form a broken diagonal: once wrapped around the original square, it can now be seen starting with the first square of the ghost image and moving down to the left.
References
- ↑ Pickover, Clifford A. (2011), The Zen of Magic Squares, Circles, and Stars: An Exhibition of Surprising Structures across Dimensions, Princeton University Press, p. 7, ISBN 9781400841516.
- ↑ Licks, H. E. (1921), Recreations in Mathematics, D. Van Nostrand Company, p. 42.