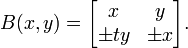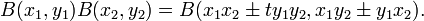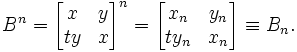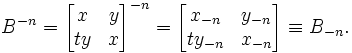Brahmagupta matrix
In mathematics, the following matrix was given by Indian mathematician Brahmagupta:[1]
It satisfies
Powers of the matrix are defined by
The 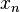 and
and 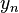 are called Brahmagupta polynomials. The Brahmagupta matrices can be extended to negative integers:
are called Brahmagupta polynomials. The Brahmagupta matrices can be extended to negative integers:
See also
- Brahmagupta's identity
- Brahmagupta's function
References
- ↑ "The Brahmagupta polynomials" (PDF). Suryanarayanan. The Fibonacci Quarterly. Retrieved 3 November 2011.
External links
- Eric Weisstein. Brahmagupta Matrix, MathWorld, 1999.
- Weisstein, Eric W. (2003). CRC Concise Encyclopedia of Mathematics. Florida: CRC Press. p. 282. ISBN 1-58488-347-2.
This article is issued from Wikipedia - version of the Sunday, June 09, 2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.