Lie algebra-valued differential form
In differential geometry, a Lie algebra-valued form is a differential form with values in a Lie algebra. Such forms have important applications in the theory of connections on a principal bundle as well as in the theory of Cartan connections.
Wedge product
Since every Lie algebra has a bilinear Lie bracket operation, the wedge product of two Lie algebra-valued forms can be composed with the bracket operation to obtain another Lie algebra-valued form. This operation, denoted by ![[\omega\wedge\eta]](../I/m/ce366be089403339a66d934dbd7a9d15.png) , is given by: for
, is given by: for 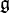 -valued p-form
-valued p-form 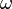 and
and 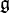 -valued q-form
-valued q-form 
where vi's are tangent vectors. The notation is meant to indicate both operations involved. For example, if 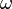 and
and  are Lie algebra-valued one forms, then one has
are Lie algebra-valued one forms, then one has
The operation ![[\omega\wedge\eta]](../I/m/ce366be089403339a66d934dbd7a9d15.png) can also be defined as the bilinear operation on
can also be defined as the bilinear operation on 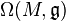 satisfying
satisfying
for all 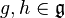 and
and 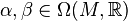 .
.
Some authors have used the notation ![[\omega, \eta]](../I/m/be2a74da7f3dd8e62e504dc7f05602f0.png) instead of
instead of ![[\omega\wedge\eta]](../I/m/ce366be089403339a66d934dbd7a9d15.png) . The notation
. The notation ![[\omega, \eta]](../I/m/be2a74da7f3dd8e62e504dc7f05602f0.png) , which resembles a commutator, is justified by the fact that if the Lie algebra
, which resembles a commutator, is justified by the fact that if the Lie algebra 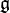 is a matrix algebra then
is a matrix algebra then ![[\omega\wedge\eta]](../I/m/ce366be089403339a66d934dbd7a9d15.png) is nothing but the graded commutator of
is nothing but the graded commutator of 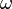 and
and  , i. e. if
, i. e. if 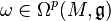 and
and 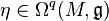 then
then
where 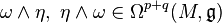 are wedge products formed using the matrix multiplication on
are wedge products formed using the matrix multiplication on 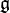 .
.
Operations
Let 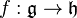 be a Lie algebra homomorphism. If φ is a
be a Lie algebra homomorphism. If φ is a 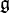 -valued form on a manifold, then f(φ) is an
-valued form on a manifold, then f(φ) is an  -valued form on the same manifold obtained by applying f to the values of φ:
-valued form on the same manifold obtained by applying f to the values of φ:  .
.
Similarly, if f is a multilinear functional on 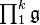 , then one puts[1]
, then one puts[1]
where q = q1 + … + qk and φi are 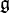 -valued qi-forms. Moreover, given a vector space V, the same formula can be used to define the V-valued form
-valued qi-forms. Moreover, given a vector space V, the same formula can be used to define the V-valued form 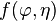 when
when
is a multilinear map, φ is a 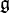 -valued form and η is a V-valued form. Note that, when
-valued form and η is a V-valued form. Note that, when
- (*) f([x, y], z) = f(x, f(y, z)) - f(y, f(x, z)),
giving f amounts to giving an action of 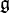 on V; i.e., f determines the representation
on V; i.e., f determines the representation
and, conversely, any representation ρ determines f with the condition (*). For example, if ![f(x, y) = [x, y]](../I/m/2e15fa21703a85a11e001501c9fb0f9f.png) (the bracket of
(the bracket of 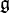 ), then we recover the definition of
), then we recover the definition of ![[\cdot \wedge \cdot]](../I/m/69665400323a4b9630422d3e57a9568d.png) given above, with ρ = ad, the adjoint representation. (Note the relation between f and ρ above is thus like the relation between a bracket and ad.)
given above, with ρ = ad, the adjoint representation. (Note the relation between f and ρ above is thus like the relation between a bracket and ad.)
In general, if α is a  -valued p-form and φ is a V-valued q-form, then one more commonly writes α⋅φ = f(α, φ) when f(T, x) = Tx. Explicitly,
-valued p-form and φ is a V-valued q-form, then one more commonly writes α⋅φ = f(α, φ) when f(T, x) = Tx. Explicitly,
With this notation, one has for example:
![\operatorname{ad}(\alpha) \cdot \phi = [\alpha \wedge \phi]](../I/m/2ce8a4ed889d63e8eb8c636eba198a74.png) .
.
Example: If ω is a 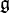 -valued one-form (for example, a connection form), ρ a representation of
-valued one-form (for example, a connection form), ρ a representation of 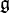 on a vector space V and φ a V-valued zero-form, then
on a vector space V and φ a V-valued zero-form, then
Forms with values in an adjoint bundle
Let P be a smooth principal bundle with structure group G and 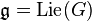 . G acts on
. G acts on 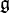 via adjoint representation and so one can form the associated bundle:
via adjoint representation and so one can form the associated bundle:
Any  -valued forms on the base space of P are in a natural one-to-one correspondence with any tensorial forms on P of adjoint type.
-valued forms on the base space of P are in a natural one-to-one correspondence with any tensorial forms on P of adjoint type.
See also
Notes
- ↑ Kobayashi–Nomizu, Ch. XII, § 1.
- ↑ Since
![\rho([\omega \wedge \omega])(v, w) = \rho([\omega \wedge \omega](v, w)) = \rho([\omega(v), \omega(w)]) = \rho(\omega(v))\rho(\omega(w)) - \rho(\omega(w))\rho(\omega(v))](../I/m/6e942b96238401dad3e232ad825927f2.png) , we have that
, we have that
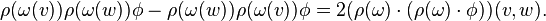
References
- S. Kobayashi, K. Nomizu. Foundations of Differential Geometry (Wiley Classics Library) Volume 1, 2.
External links
- http://mathoverflow.net/questions/123632/wedge-product-of-lie-algebra-valued-one-form
- http://ncatlab.org:8080/nlab/show/groupoid+of+Lie-algebra+valued+forms
 = {1 \over (p + q)!}\sum_{\sigma} \operatorname{sgn}(\sigma) [\omega(v_{\sigma(1)}, \cdots, v_{\sigma(p)}), \eta(v_{\sigma(p+1)}, \cdots, v_{\sigma(p+q)})]](../I/m/d0940f4ab1a699d68714f324b6dd50d0.png)
 = {1 \over 2} ([\omega(v_1),\eta(v_2)] - [\omega(v_2),\eta(v_1)]).](../I/m/36b8faa696e10ac6044f3a93afcdf449.png)
![[(g \otimes \alpha) \wedge (h \otimes \beta)] = [g, h] \otimes (\alpha \wedge \beta)](../I/m/254343088d87e3da5d3e0c6345c3486e.png)
![[\omega\wedge\eta] = \omega\wedge\eta - (-1)^{pq}\eta\wedge\omega,](../I/m/9e6d8c000a9219928eaabc79146f0c12.png)
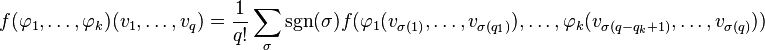
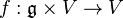
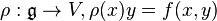
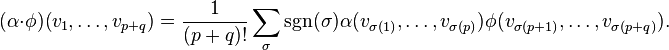
![\rho([\omega \wedge \omega]) \cdot \varphi = 2 \rho(\omega) \cdot (\rho(\omega) \cdot \varphi).](../I/m/3275e1bc9566140b0606626d9c160d02.png)
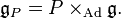
![(\rho([\omega \wedge \omega]) \cdot \phi)(v, w) = {1 \over 2} (\rho([\omega \wedge \omega])(v, w) \phi - \rho([\omega \wedge \omega])(w, v) \phi)](../I/m/ced12e765794e8393b420ce4a047940e.png)