Bott–Samelson resolution

In algebraic geometry, the Bott–Samelson resolution of a Schubert variety is a resolution of singularities. It was introduced by (Bott–Samelson 1959) in the context of compact Lie groups.^[1] The algebraic formulation is due to (Hansen 1973) and (Demazure 1974).

Definition

Let G be a connected reductive complex algebraic group, B a Borel subgroup and T a maximal torus contained in B.

Let 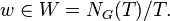$w \in W = N_G(T)/T.$ Any such w can be written as a product of reflections by simple roots. Fix minimal such an expression:

\underline{w} = (s_{i_1}, s_{i_2}, \ldots, s_{i_l})

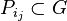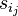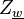so that $w = s_{i_1} s_{i_2} \cdots s_{i_l}$ . (l is the length of w.) Let $P_{i_j} \subset G$ be the subgroup generated by B and a representative of $s_{i_j}$ . Let $Z_{\underline{w}}$ be the quotient:

Z_{\underline{w}} = P_{i_1} \times \cdots \times P_{i_l}/B^l

with respect to the action of $B^l$ by

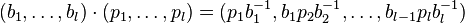(b_1, \ldots, b_l) \cdot (p_1, \ldots, p_l) = (p_1 b_1^{-1}, b_1 p_2 b_2^{-1}, \ldots, b_{l-1} p_l b_l^{-1})

It is a smooth projective variety. Writing $X_w = \overline{BwB} / B = (P_{i_1} \cdots P_{i_l})/B$ for the Schubert variety for w, the multiplication map

\pi: Z_{\underline{w}} \to X_w

is a resolution of singularities called the Bott–Samelson resolution. 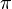$\pi$ has the property: 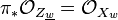$\pi_* \mathcal{O}_{Z_{\underline{w}}} = \mathcal{O}_{X_w}$ and $R^i \pi_* \mathcal{O}_{Z_{\underline{w}}} = 0, \, i \ge 1.$ In other words, $X_w$ has rational singularities.^[2]

There are also some other constructions; see, for example, (Vakil 2006).

Notes

↑ Gorodski, Claudio; Thorbergsson, Gudlaugur (2001-01-25). "Cycles of Bott-Samelson type for taut representations". arXiv:math/0101209.
↑ Brion 2005, Theorem 2.2.3.

References

R. Bott and H. Samelson, Application of the theory of Morse to symmetric spaces, Amer. J. Math. 80 (1958), 964–1029.
Brion, M., Lectures on the geometry of flag varieties, Trends Math., Birkhäuser, Basel, 2005.
M. Demazure, Désingularisations des variétés de Schubert généralisées, Ann. Sci. Éc. Norm. Supér. 7 (1974), 53–88.
H. C. Hansen, On cycles in flag manifolds, Math. Scand. 33 (1973), 269–274.
R. Vakil, A geometric Littlewood-Richardson rule, arXiv:math.AG/0302294. the Annals of Math. (2006)

This article is issued from Wikipedia - version of the Monday, November 23, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.