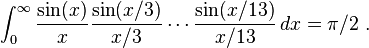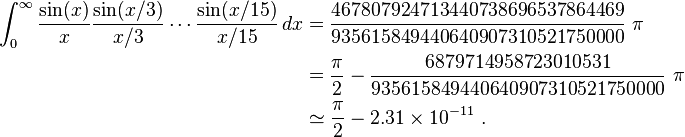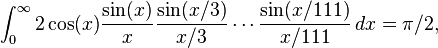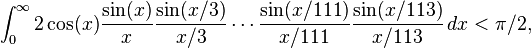Borwein integral

In mathematics, a Borwein integral is an integral involving products of sinc(ax), where the sinc function is given by sinc(x) = sin(x)/x for x not equal to 0, and sinc(0) = 1.[1][2]

These integrals are remarkable for exhibiting apparent patterns which, however, eventually break down. An example is as follows,

\begin{align} & \int_0^\infty \frac{\sin(x)}{x} \, dx=\pi/2 \\[10pt] & \int_0^\infty \frac{\sin(x)}{x}\frac{\sin(x/3)}{x/3} \, dx = \pi/2 \\[10pt] & \int_0^\infty \frac{\sin(x)}{x}\frac{\sin(x/3)}{x/3}\frac{\sin(x/5)}{x/5} \, dx = \pi/2 \end{align}

This pattern continues up to

\int_0^\infty \frac{\sin(x)}{x}\frac{\sin(x/3)}{x/3}\cdots\frac{\sin(x/13)}{x/13} \, dx = \pi/2 ~.

Nevertheless, at the next step the obvious pattern fails,

\begin{align} \int_0^\infty \frac{\sin(x)}{x}\frac{\sin(x/3)}{x/3}\cdots\frac{\sin(x/15)}{x/15} \, dx &= \frac{467807924713440738696537864469}{935615849440640907310521750000}~\pi \\ &= \frac{\pi}{2} - \frac{6879714958723010531}{935615849440640907310521750000}~\pi \\ &\simeq \frac{\pi}{2} - 2.31\times 10^{-11} ~. \end{align}

In general, similar integrals have value π/2 whenever the numbers 3, 5, 7… are replaced by positive real numbers such that the sum of their reciprocals is less than 1.

In the example above, 1/3 + 1/5 + … + 1/13 < 1, but 1/3 + 1/5 + … + 1/15 > 1.

An example for a longer series,

\int_0^\infty 2 \cos(x) \frac{\sin(x)}{x}\frac{\sin(x/3)}{x/3}\cdots\frac{\sin(x/111)}{x/111} \, dx = \pi/2,

but

\int_0^\infty 2 \cos(x) \frac{\sin(x)}{x}\frac{\sin(x/3)}{x/3}\cdots\frac{\sin(x/111)}{x/111}\frac{\sin(x/113)}{x/113} \, dx < \pi/2,

is shown in [3] together with an intuitive mathematical explanation of the reason why the original and the extended series break down. In this case, 1/3 + 1/5 + … + 1/111 < 2, but 1/3 + 1/5 + … + 1/113 > 2.

References

  1. ↑ Borwein, David; Borwein, Jonathan M. (2001), "Some remarkable properties of sinc and related integrals", The Ramanujan Journal 5 (1): 73–89, doi:10.1023/A:1011497229317, ISSN 1382-4090, MR 1829810
  2. ↑ Baillie, Robert (2011). "Fun With Very Large Numbers". arXiv:1105.3943 [math.NT].
  3. ↑ Schmid, Hanspeter (2014), "Two curious integrals and a graphic proof" (PDF), Elemente der Mathematik 69 (1): 11–17, doi:10.4171/EM/239, ISSN 0013-6018
This article is issued from Wikipedia - version of the Friday, January 22, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.