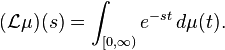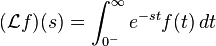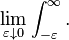Borel measure

In mathematics, specifically in measure theory, a Borel measure on a topological space is a measure that is defined on all open sets (and thus on all Borel sets).^[1] Some authors require additional restrictions on the measure, as described below.

Formal definition

Let X be a locally compact Hausdorff space, and let 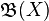$\mathfrak{B}(X)$ be the smallest σ-algebra that contains the open sets of X; this is known as the σ-algebra of Borel sets. A Borel measure is any measure μ defined on the σ-algebra of Borel sets.^[2] Some authors require in addition that μ(C) < ∞ for every compact set C. If a Borel measure μ is both inner regular and outer regular, it is called a regular Borel measure (some authors also require it to be tight). If μ is both inner regular and locally finite, it is called a Radon measure. Note that a locally finite Borel measure automatically satisfies μ(C) < ∞ for every compact set C.

On the real line

The real line 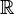$\mathbb R$ with its usual topology is a locally compact Hausdorff space, hence we can define a Borel measure on it. In this case, 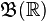$\mathfrak{B}(\mathbb R)$ is the smallest σ-algebra that contains the open intervals of 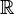$\mathbb R$ . 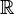While there are many Borel measures μ, the choice of Borel measure which assigns $\mu([a,b])=b-a$ for every interval $[a,b]$ is sometimes called "the" Borel measure on $\mathbb R$ . In practice, even "the" Borel measure is not the most useful measure defined on the σ-algebra of Borel sets; indeed, the Lebesgue measure $\lambda$ is an extension of "the" Borel measure which possesses the crucial property that it is a complete measure (unlike the Borel measure). 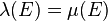To clarify, when one says that the Lebesgue measure $\lambda$ is an extension of the Borel measure $\mu$ , it means that every Borel-measurable set E is also a Lebesgue-measurable set, and the Borel measure and the Lebesgue measure coincide on the Borel sets (i.e., $\lambda(E)=\mu(E)$ for every Borel measurable set).

Product spaces

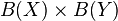If X and Y are second-countable, Hausdorff topological spaces, then the set of Borel subsets $B(X\times Y)$ of their product coincides with the product of the sets $B(X)\times B(Y)$ of Borel subsets of X and Y.^[3] That is, the Borel functor

\mathbf{Bor}\colon\mathbf{Top}_{2CHaus}\to\mathbf{Meas}

from the category of second-countable Hausdorff spaces to the category of measurable spaces preserves finite products.

Applications

Lebesgue–Stieltjes integral

Main article: Lebesgue–Stieltjes integral

The Lebesgue–Stieltjes integral is the ordinary Lebesgue integral with respect to a measure known as the Lebesgue–Stieltjes measure, which may be associated to any function of bounded variation on the real line. The Lebesgue–Stieltjes measure is a regular Borel measure, and conversely every regular Borel measure on the real line is of this kind.^[4]

Laplace transform

Main article: Laplace transform

One can define the Laplace transform of a finite Borel measure μ on the real line by the Lebesgue integral^[5]

(\mathcal{L}\mu)(s) = \int_{[0,\infty)} e^{-st}\,d\mu(t).

An important special case is where μ is a probability measure or, even more specifically, the Dirac delta function. In operational calculus, the Laplace transform of a measure is often treated as though the measure came from a distribution function f. In that case, to avoid potential confusion, one often writes

(\mathcal{L}f)(s) = \int_{0^-}^\infty e^{-st}f(t)\,dt

where the lower limit of 0⁻ is shorthand notation for

\lim_{\varepsilon\downarrow 0}\int_{-\varepsilon}^\infty.

This limit emphasizes that any point mass located at 0 is entirely captured by the Laplace transform. Although with the Lebesgue integral, it is not necessary to take such a limit, it does appear more naturally in connection with the Laplace–Stieltjes transform.

Hausdorff dimension and Frostman's lemma

Main articles: Hausdorff dimension and Frostman's lemma

Given a Borel measure μ on a metric space X such that μ(X) > 0 and μ(B(x, r)) ≤ r^s holds for some constant s > 0 and for every ball B(x, r) in X, then the Hausdorff dimension dim_Haus(X) ≥ s. A partial converse is provided by Frostman's lemma:^[6]

Lemma: Let A be a Borel subset of Rⁿ, and let s > 0. Then the following are equivalent:

H^s(A) > 0, where H^s denotes the s-dimensional Hausdorff measure.
There is an (unsigned) Borel measure μ satisfying μ(A) > 0, and such that

\mu(B(x,r))\le r^s

holds for all x ∈ Rⁿ and r > 0.

Cramér–Wold theorem

Main article: Cramér–Wold theorem

The Cramér–Wold theorem in measure theory states that a Borel probability measure on 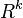$R^k$ is uniquely determined by the totality of its one-dimensional projections.^[7] It is used as a method for proving joint convergence results. The theorem is named after Harald Cramér and Herman Ole Andreas Wold.

References

↑ D. H. Fremlin, 2000. Measure Theory. Torres Fremlin.
↑ Alan J. Weir (1974). General integration and measure. Cambridge University Press. pp. 158–184. ISBN 0-521-29715-X.
↑ Vladimir I. Bogachev. Measure Theory, Volume 1. Springer Science & Business Media, Jan 15, 2007
↑ Halmos, Paul R. (1974), Measure Theory, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90088-9
↑ Feller 1971, §XIII.1
↑ Rogers, C. A. (1998). Hausdorff measures. Cambridge Mathematical Library (Third ed.). Cambridge: Cambridge University Press. pp. xxx+195. ISBN 0-521-62491-6.
↑ K. Stromberg, 1994. Probability Theory for Analysts. Chapman and Hall.

External links

Borel measure at Encyclopedia of Mathematics

This article is issued from Wikipedia - version of the Monday, November 16, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.