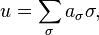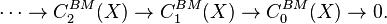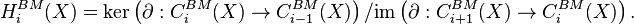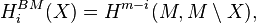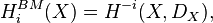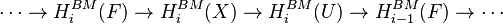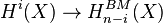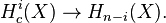Borel–Moore homology
In topology, Borel−Moore homology or homology with closed support is a homology theory for locally compact spaces, introduced by Borel and Moore (1960).
For reasonable compact spaces, Borel−Moore homology coincides with the usual singular homology. For non-compact spaces, each theory has its own advantages. In particular, a closed oriented submanifold defines a class in Borel–Moore homology, but not in ordinary homology unless the submanifold is compact.
Note: The equivariant cohomology theory for spaces with an action of a group G is sometimes called Borel cohomology; it is defined as H*G(X) = H*((EG × X)/G). That is not related to the subject of this article.
Definition
There are several ways to define Borel−Moore homology. They all coincide for reasonable spaces such as manifolds and CW complexes.
Definition via sheaf cohomology
For any locally compact space X, Borel-Moore homology with integral coefficients is defined as the cohomology of the dual of the chain complex which computes sheaf cohomology with compact support.[1] As a result, there is a short exact sequence analogous to the universal coefficient theorem:
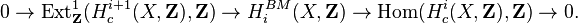
In what follows, the coefficients Z are not written.
Definition via locally finite chains
The singular homology of a topological space X is defined as the homology of the chain complex of singular chains, that is, finite linear combinations of continuous maps from the simplex to X. The Borel−Moore homology of a reasonable locally compact space X, on the other hand, is isomorphic to the homology of the chain complex of locally finite singular chains. "Reasonable" means here that X is locally contractible, σ-compact, and of finite dimension.[2]
In more detail, let CiBM(X) be the abelian group of formal (infinite) sums
where σ runs over the set of all continuous maps from the standard i-simplex Δi to X and each aσ is an integer, such that for each compact subset S of X, only finitely many maps σ whose image meets S have nonzero coefficient in u. Then the usual definition of the boundary ∂ of a singular chain makes these abelian groups into a chain complex:
The Borel−Moore homology groups HiBM(X) are the homology groups of this chain complex. That is,
If X is compact, then every locally finite chain is in fact finite. So, given that X is "reasonable" in the sense above, Borel−Moore homology HiBM(X) coincides with the usual singular homology Hi(X) for X compact.
Definition via compactifications
Suppose that X is homeomorphic to the complement of a closed subcomplex S in a finite CW complex Y. Then Borel–Moore homology HiBM(X) is isomorphic to the relative homology Hi(Y, S). Under the same assumption on X, the one-point compactification of X is homeomorphic to a finite CW complex. As a result, Borel–Moore homology can be viewed as the relative homology of the one-point compactification with respect to the added point.
Definition via Poincaré duality
Let X be any locally compact space with a closed embedding into an oriented manifold M of dimension m. Then
where in the right hand side, the usual relative cohomology is meant.[3]
Definition via the dualizing complex
For any locally compact space X of finite dimension, let DX be the dualizing complex of X. Then
where in the right hand side, hypercohomology is meant.[4]
Example
Let X = R2 − 0, the plane minus the origin. The usual homology of X is Z in degrees 0 and 1 (and zero otherwise), while the Borel−Moore homology of X is Z in degrees 1 and 2 (and zero otherwise). In this example, the natural homomorphism Hi(X) → HiBM(X) is zero for all integers i. For example, the usual homology H1(X) is generated by a circle around the origin, but this maps to zero in Borel–Moore homology, because a finite 1-chain representing the circle is the boundary of a locally finite 2-chain whose image is the region inside the circle. The Borel–Moore homology H1BM(X) is generated by a locally finite 1-chain whose image is (for example) the ray from 0 to ∞ in the real line R inside R2.
Properties
- Borel−Moore homology is a covariant functor with respect to proper maps. That is, a proper map f: X → Y induces a pushforward homomorphism HiBM(X) → HiBM(Y) for all integers i. In contrast to ordinary homology, there is no pushforward on Borel−Moore homology for an arbitrary continuous map f. As a counterexample, one can consider the non-proper inclusion R2 − 0 → R2.
- Borel−Moore homology is a contravariant functor with respect to inclusions of open subsets. That is, for U open in X, there is a natural pullback or restriction homomorphism HiBM(X) → HiBM(U).
- For any locally compact space X and any closed subset F, with U = X − F the complement, there is a long exact localization sequence:[5]
- Borel−Moore homology is homotopy invariant in the sense that for any space X, there is an isomorphism HiBM(X) → Hi+1BM(X × R). The shift in dimension means that Borel−Moore homology is not homotopy invariant in the naive sense. For example, the Borel−Moore homology of Euclidean space Rn is isomorphic to Z in degree n and is otherwise zero.
- Poincaré duality extends to non-compact manifolds using Borel–Moore homology. Namely, for an oriented n-manifold X, Poincaré duality is an isomorphism
for all integers i. A different version of Poincaré duality for non-compact manifolds is the isomorphism from cohomology with compact support to usual homology:
- A key advantage of Borel−Moore homology is that every oriented manifold M of dimension n (in particular, every smooth complex algebraic variety), not necessarily compact, has a fundamental class [M] ∈ HnBM(M). This is just the sum of all top dimensional simplices in a specific triangulation. In fact, in Borel−Moore homology, one can define a fundamental class for arbitrary (possibly singular) complex varieties. In this case the set of smooth points Mreg ⊂ M has complement of (real) codimension at least 2, and by the long exact sequence above the top dimensional homologies of M and Mreg are canonically isomorphic. The fundamental class of M is then defined to be the fundamental class of Mreg.[6]
Notes
- ↑ B. Iversen. Cohomology of sheaves. Section IX.1.
- ↑ G. Bredon. Sheaf theory. Corollary V.12.21.
- ↑ B. Iversen. Cohomology of sheaves. Theorem IX.4.7.
- ↑ B. Iversen. Cohomology of sheaves. Equation IX.4.1.
- ↑ B. Iversen. Cohomology of sheaves. Equation IX.2.1.
- ↑ W. Fulton. Intersection theory. Lemma 19.1.1.
References
- Borel, Armand; Moore, John C. (1960), "Homology theory for locally compact spaces", The Michigan Mathematical Journal 7: 137–159, doi:10.1307/mmj/1028998385, ISSN 0026-2285, MR 0131271
- Bredon, Glen E. (1997), Sheaf theory (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-94905-5, MR 1481706
- Fulton, William (1998), Intersection theory (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-62046-4, MR 1644323
- Iversen, Birger (1986), Cohomology of sheaves, Berlin: Springer-Verlag, ISBN 3-540-16389-1, MR 0842190