Book (graph theory)
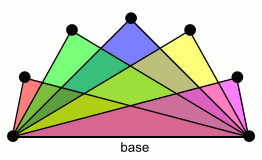
In graph theory, a book graph (often written 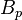 ) may be any of several kinds of graph.
) may be any of several kinds of graph.
One kind, which may be called a quadrilateral book, consists of p quadrilaterals sharing a common edge (known as the "spine" or "base" of the book).[1] A book of this type is the Cartesian product of a star and K2 .
A second type, which might be called a triangular book, is the complete tripartite graph K1,1,p. It is a graph consisting of  triangles sharing a common edge.[2] A book of this type is a split graph.
This graph has also been called a
triangles sharing a common edge.[2] A book of this type is a split graph.
This graph has also been called a 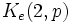 .[3]
.[3]
Given a graph  , one may write
, one may write 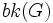 for the largest book (of the kind being considered) contained within
for the largest book (of the kind being considered) contained within  .
.
The term "book-graph" has been employed for other uses. Barioli[4] used it to mean a graph composed of a number of arbitrary subgraphs having two vertices in common. (Barioli did not write 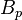 for his book-graph.)
for his book-graph.)
Theorems on books
Denote the Ramsey number of two (triangular) books by 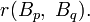
- There exists a constant
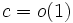 such that
such that 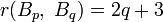 whenever
whenever 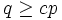 .
. - If
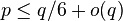 , and
, and 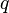 is large, the Ramsey number is given by
is large, the Ramsey number is given by 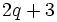 .
.
- Let
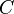 be a constant, and
be a constant, and 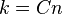 . Then every graph on
. Then every graph on  vertices and
vertices and  edges contains a (triangular)
edges contains a (triangular)  .[5]
.[5]
References
- ↑ Eric W. Weisstein, "Book Graph." From MathWorld–A Wolfram Web Resource.
- ↑ Lingsheng Shi and Zhipeng Song, Upper bounds on the spectral radius of book-free and/or K2,l-free graphs. Linear Algebra and its Applications, vol. 420 (2007), pp. 526–529. doi:10.1016/j.laa.2006.08.007
- ↑ Erdős, Paul (1963). "On the structure of linear graphs". Israel Journal of Mathematics 1: 156–160. doi:10.1007/BF02759702.
- ↑ Francesco Barioli, Completely positive matrices with a book-graph. Linear Algebra and its Applications, vol. 277 (1998), pp. 11–31. doi:10.1016/S0024-3795(97)10070-2
- ↑ P. Erdos, On a theorem of Rademacher-Turán. Illinois Journal of Mathematics, vol. 6 (1962), pp. 122–127.
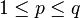 , then
, then