Bispectrum
In mathematics, in the area of statistical analysis, the bispectrum is a statistic used to search for nonlinear interactions.
Definitions
The Fourier transform of the second-order cumulant, i.e., the autocorrelation function, is the traditional power spectrum.
The Fourier transform of C3(t1, t2) (third-order cumulant-generating function) is called the bispectrum or bispectral density.
Calculation
Applying the convolution theorem allows fast calculation of the bispectrum 
, where 
denotes the Fourier transform of the signal, and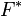 
its conjugate.
Generalizations
Bispectra fall in the category of higher-order spectra, or polyspectra and provide supplementary information to the power spectrum. The third order polyspectrum (bispectrum) is the easiest to compute, and hence the most popular.
A statistic defined analogously is the bispectral coherency or bicoherence.
Applications
Bispectrum and bicoherence may be applied to the case of non-linear interactions of a continuous spectrum of propagating waves in one dimension.[1]
Bispectral measurements have been carried out for EEG signals monitoring.[2] It was also shown that bispectra characterize differences between families of musical instruments.[3]
In seismology, signals rarely have adequate duration for making sensible bispectral estimates from time averages.
See also
References
- ↑ Greb U, Rusbridge MG (1988). "The interpretation of the bispectrum and bicoherence for non-linear interactions of continuous spectra". Plasma Phys. Control. Fusion 30 (5): 537–49. doi:10.1088/0741-3335/30/5/005.
- ↑ Johansen JW, Sebel PS (November 2000). "Development and clinical application of electroencephalographic bispectrum monitoring". Anesthesiology 93 (5): 1336–44. doi:10.1097/00000542-200011000-00029. PMID 11046224.
- ↑ Dubnov S, Tishby N and Cohen D. (1997). "Polyspectra as Measures of Sound Texture and Timbre". Journal of New Music Research 26: 277–314. doi:10.1080/09298219708570732.
- Mendel JM. "Tutorial on higher-order statistics (spectra) in signal processing and system theory: theoretical results and some applications". Proc. IEEE 79 (3): 278–305. doi:10.1109/5.75086.
- HOSA - Higher Order Spectral Analysis Toolbox: A MATLAB toolbox for spectral and polyspectral analysis, and time-frequency distributions. The documentation explains polyspectra in great detail.