Bioheat transfer

Bioheat transfer is the study of heat transfer in biological systems. In simpler terms, it is the study of how heat moves from one compartment, be it within the body or external to the body, to another compartment in the body. Bioheat transfer has its foundations in the engineering discipline of heat transfer and is itself a subfield of biomedical engineering or bioengineering. In addition, computational techniques to model various bioheat transfer scenarios are widely employed and hold an important place in developing devices and protocols for the medical community.

Constitutive Values

Because modeling bioheat transfer is of the utmost importance in proper device or heating protocol design, constitutive values of various tissues of the body had to be measured early on in the history of bioheat transfer.

Of particular importance were the values of specific gravity, specific heat, thermal conductivity for the various tissues in the body e.g. skin, fat, muscle, bone, and blood. Today, such values can be easily found in various handbooks and study publications such as the CRC Handbook of Mechanical Engineering (2nd Ed.) or the Report of the task group on reference man (1975).

To illustrate the detailed knowledge that is required by the bioheat transfer community, The CRC Handbook of Mechanical Engineering includes a nearly 2 page table of value for thermal conductivity of various organs including but not limited to: kidney, aorta, arterial plaque, blood, liver, spleen, heart, muscle and tumor.

Because of the importance of blood perfusion on thermal equilibria in the body, blood perfusion values were also pursued early in the history of the field. The CRC Handbook of Mechanical Engineering's chapter on Bioheat Transfer includes a nearly 6 page table of blood perfusion values for a similar variety of tissues as the table for thermal conductivity. Greater discussion on the effect of blood perfusion on heat transfer is given in Section 2.

The Cardiovascular System

The cardiovascular system is the key system by which heat is distributed throughout the body. The blood serves as the vehicle to transport heat from the areas of high heat to areas of lower heat. In general this transfer takes place in the direction from body core to extremities such as the limbs and head. In the case where the extremities are hotter than the core body temperature, perfusion would serve to transport heat from the extremity back towards the body core. Whether or not the core temperature rises depends on many factors such as the duration of elevated local temperature at the extremity, temperature difference between extremity and core, volume of blood heated above core temperature, and the rate of blood perfusion. This same moderating phenomena of blood perfusion can be applied to local heat transfer problems e.g. heating of a tumor.

Ablative Surgical Procedures

Ablative surgical techniques generally employ some method of energy deposition which destroys cells and tissue with a concomitant increase in temperature at the targeted site. Bioheat transport equations can be applied to the process of energy deposition into the tissue as well as the subsequent conduction/convection heat transport to cells neighboring the targeted site to predict a temperature history and distribution. Such a model could be used to select the most appropriate protocol for the surgery.

Various modalities of energy deposition include: radio frequency, laser, high intensity focused ultrasound, etc. These modalities are commonly used in the minimally invasive surgical treatment of cancer.[1] One common type is radiofrequency ablation, a type of hyperthermia therapy.

Cryosurgical Procedures

Cryosugery is a technique which employs the use of low temperatures to destroy cells. The mechanism of death is usually by plasma membrane and protein disruption via physical and osmotic damage when ice crystals form within the cytoplasm of the cell. Bioheat transport equations can also be used to model this process.

Therapeutic Hyperthermia & Hypothermia

Heat can be used not only to destroy cells, but also to aid in the recovery of cells and tissues. Such use of heat is sometimes called therapeutic hyperthermia, perhaps to distinguish it from malignant hyperthermia.

An example of therapeutic hyperthermia is the ThermaCare HeatWrap by Procter & Gamble. The application of heat to injured tissues works to heal target tissues by a temperature dependent vasodilation. This vasodilation increases the mass transport of wastes and nutrients from and to the site of injury. Because damaged tissue is more metabolically active the enhanced mass transport can facilitate more rapid healing.

Hypothermia
Heat transfer is not only study of raising temperatures, but also reducing them. It is commonly understood that lower temperatures help to preserve living or "once living" tissue. For example, foods stored in refrigerators last longer because the metabolic processes of cellular decay and bacterial growth are slowed due to the lower free energy (e.g. heat) in the refrigerator. This principle is often applied in surgical wards to individuals who experience head trauma.

In cases of head trauma, it is common procedure to reduce the body temperature to about 32°C (90°F) which is about 5°C (8.5°F) lower than normal core temperature of 37°C (98.5°F). This presents a good example of how bioheat transfer engineers can contribute to medical treatments. Such a situation would be broken down first into a system, which in this case would include the entire surface of the body. Assuming the individual is submerged in cold water up to the neck and ears, or otherwise surrounded by an environment that can be modeled as a temperature sink, the engineering would model the body as a composite system composed of skin, fat, muscle bone and possibly organs depending on how complex the model must be. The head could be considered a separate system connected to the body via a third major system, the vasculature. The vasculature would bring cooled blood from the submerged body to the brain where there would be some amount of conductive and convection heat transfer based on the passage of blood through the vessels cooling the vessel via forced convection and the subsequent cooling of the brain via conduction between blood vessel and brain tissue. Each of these heat transfer processes i.e. water to body, body to vasculature, and vasculature to brain would require knowledge of the thermal conductivity, specific heat, density, blood perfusion rate, and diameter of blood vessel at the least to predict the temperature history at any point within the body e.g. to know when the temperature at the center of the head trauma reaches 32°C.

Such application of hypothermia is also employed during open heart surgery where perfusion to the body and brain must stop while cardiac output is rerouted through a heart lung machine. Furthermore, biomedical engineers who specialize in bioheat transfer are able to design such medical devices to perform within a specified range of temperatures and rates of cooling.

Cryopreservation

Bioheat Models

Here we present a simplified model of the bioheat equation for steady-state, one-dimensional heat transfer. From a one-dimensional energy balance in the x-direction:

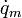\frac{d^2 T}{dx^2} + \frac{\dot{q}_m + \dot{q}_p}{k}=0 \quad [1] [2]

Where \dot{q}_m is the metabolic heat source term and 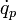\dot{q}_p is the perfusion heat source term, both per unit volume. The thermal conductivity, k, is a constant.

Pennes proposed an expression for the perfusion term by assuming that the temperatures of blood entering and exiting capillaries are both constant for any small volume of tissue. We can say that the temperatures of the blood at each state are the same as that of the surroundings, namely the arterial temperature and the local tissue temperature. Now we must define the perfusion rate, 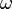\omega. This is the ratio of the volumetric flow rate of blood per volume of tissue. Thus we have for the perfusion term:

\dot{q}_p=\omega \rho_b c_b (T_a-T) \quad [2] [2]

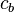Where \rho_b and c_b are the density and specific heat capacity of the blood, respectively.

Combining these two equations results in:

\frac{d^2 T}{dx^2} + \frac{\dot{q}_m + \omega \rho_b c_b (T_a-T)}{k}=0 \quad [3] [2]

Which is the Pennes Bioheat Equation for one-dimensional, steady-state, heat transfer.

Training

Most people that work in the field of bioheat transfer can be considered biomedical engineers. A number of universities grant bachelor's degrees in biomedical engineering and bioengineering, but due to the large variety of sub-fields in biomedical engineering the training that undergraduate students receive varies greatly from program to program. Most engineers who have expertise in bioheat transfer received training from academic research labs either as undergraduates or as graduate students.

Additional resources

References

  1. ↑ Kuznetsov, A.V. (2006). "Optimization problems for bioheat equation". International Communications in Heat and Mass Transfer 33 (5): 537–543. doi:10.1016/j.icheatmasstransfer.2006.01.012.
  2. 1 2 3 Introduction to Heat Transfer, 5th ed. Incropera, DeWitt, Bergman, Lavine. Wiley, 2007. ISBN 978-0-471-45727-5

External links

This article is issued from Wikipedia - version of the Sunday, December 20, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.