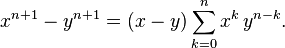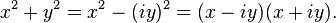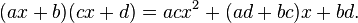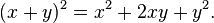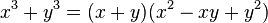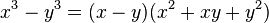Binomial (polynomial)

For other uses, see Binomial.

In algebra, a binomial is a polynomial that is the sum of two terms, each of which is a monomial.^[1] It is the simplest kind of polynomial after the monomials.

Definition

A binomial is a polynomial which is the sum of two monomials. A binomial in a single indeterminate (also known as a univariate binomial) can be written in the form

a x^m - bx^n \,,

where $a$ and $b$ are numbers, and $m$ and $n$ are distinct nonnegative integers and $x$ is a symbol which is called an indeterminate or, for historical reasons, a variable. In the context of Laurent polynomials, a Laurent binomial, often simply called a binomial, is similarly defined, but the exponents $m$ and $n$ may be negative.

More generally, a binomial may be written^[2] as:

a x_1^{n_1}\dotsb x_i^{n_i} - b x_1^{m_1}\dotsb x_i^{m_i}

Some examples of binomials are:

3x - 2x^2

xy + yx^2

0.9 x^3 + \pi y^2

Operations on simple binomials

The binomial $x 2 - y 2$ can be factored as the product of two other binomials:

x^2 - y^2 = (x + y)(x - y).

This is a special case of the more general formula:

x^{n+1} - y^{n+1} = (x - y)\sum_{k=0}^{n} x^{k}\,y^{n-k}.

When working over the complex numbers, this can also be extended to:

x^2 + y^2 = x^2 - (iy)^2 = (x - iy)(x + iy).

The product of a pair of linear binomials $(ax + b)$ and $(cx + d)$ is a trinomial:

(ax+b)(cx+d) = acx^2+(ad+bc)x+bd.

A binomial raised to the $n$ ^th power, represented as $(x + y) n$ can be expanded by means of the binomial theorem or, equivalently, using Pascal's triangle. For example, the square $(x + y) 2$ of the binomial $(x + y)$ is equal to the sum of the squares of the two terms and twice the product of the terms, that is:

(x + y)^2 = x^2 + 2xy + y^2.

The numbers (1, 2, 1) appearing as multipliers for the terms in this expansion are binomial coefficients two rows down from the top of Pascal's triangle. The expansion of the

n

^th power uses the numbers

n

rows down from the top of the triangle.

An application of above formula for the square of a binomial is the " $(m, n)$ -formula" for generating Pythagorean triples:

For

m < n

, let

a = n 2 - m 2

b = 2 mn

, and

c = n 2 + m 2

; then

a 2 + b 2 = c 2

Binomials that are sums or differences of cubes can be factored into lower-order polynomials as follows:

x^3 + y^3 = (x + y)(x^2 - xy + y^2)

x^3 - y^3 = (x - y)(x^2 + xy + y^2)

Notes

↑ Weisstein, Eric. "Binomial". Wolfram MathWorld. Retrieved 29 March 2011.
↑ Sturmfels, Bernd (2002). "Solving Systems of Polynomial Equations". CBMS Regional Conference Series in Mathematics (Conference Board of the Mathematical Sciences) (97): 62. Retrieved 21 March 2014.

References

Bostock, L.; Chandler, S. (1978). Pure Mathematics 1. Oxford University Press. p. 36. ISBN 0-85950-092-6.

Polynomials and polynomial functions

By degree	Zero polynomial (degree undefined or −1 or −∞) Constant function (0) Linear function (1) Quadratic function (2) Cubic function (3) Quartic function (4) Quintic function (5) Sextic equation (6) Septic equation (7) Octic equation (8)

By number of terms	Monomial Binomial Trinomial

Algorithms	Factorization Greatest common divisor Division Horner's method of evaluation Resultant Discriminant Gröbner basis

This article is issued from Wikipedia - version of the Wednesday, January 20, 2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Binomial (polynomial)

Definition

Operations on simple binomials

See also

Notes

References