Binary game

In mathematics, the binary game is a topological game introduced by Stanislaw Ulam in 1935 in an addendum to problem 43 of the Scottish book as a variation of the Banach–Mazur game.

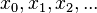In the binary game, one is given a fixed subset X of the set {0,1}^N of all sequences of 0s and 1s. The players take it in turn to choose a digit 0 or 1, and the first player wins if the sequence they form lies in the set X. Another way to represent this game is to pick a subset $X$ of the interval $[0,2]$ on the real line, then the players alternatively choose binary digits $x_0, x_1, x_2, ...$ . Player I wins the game if and only if the binary number 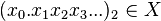$(x_0{}.x_1{}x_2{}x_3{}...)_2 \in{}X$ , that is, 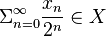$\Sigma^{\infty}_{n=0}\frac{x_n}{2^n}\in{}X$ . See,^[1] page 237.

The binary game is sometimes called Ulam's game, but "Ulam's game" usually refers to the Rényi–Ulam game.

References

↑ Telgársky, Rastislav (Spring 1987). "Topological Games: On the 50th Anniversary of the Banach-Mazur Game" (PDF). Rocky Mountain Journal of Mathematics 17 (2): 227–276.

This article is issued from Wikipedia - version of the Wednesday, November 25, 2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.