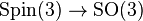Binary cyclic group

In mathematics, the binary cyclic group of the n-gon is the cyclic group of order 2n, 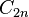C_{2n}, thought of as an extension of the cyclic group C_n by a cyclic group of order 2. It is the binary polyhedral group corresponding to the cyclic group.[1]

In terms of binary polyhedral groups, the binary cyclic group is the preimage of the cyclic group of rotations (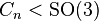C_n < \operatorname{SO}(3)) under the 2:1 covering homomorphism

\operatorname{Spin}(3) \to \operatorname{SO}(3)\,

of the special orthogonal group by the spin group.

As a subgroup of the spin group, the binary cyclic group can be described concretely as a discrete subgroup of the unit quaternions, under the isomorphism 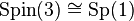\operatorname{Spin}(3) \cong \operatorname{Sp}(1) where Sp(1) is the multiplicative group of unit quaternions. (For a description of this homomorphism see the article on quaternions and spatial rotations.)

See also

References

  1. ↑ Coxeter, H. S. M. (1959), "Symmetrical definitions for the binary polyhedral groups", Proc. Sympos. Pure Math., Vol. 1, Providence, R.I.: American Mathematical Society, pp. 64–87, MR 0116055.


This article is issued from Wikipedia - version of the Monday, May 05, 2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.