Bin packing problem
In the bin packing problem, objects of different volumes must be packed into a finite number of bins or containers each of volume V in a way that minimizes the number of bins used. In computational complexity theory, it is a combinatorial NP-hard problem.
There are many variations of this problem, such as 2D packing, linear packing, packing by weight, packing by cost, and so on. They have many applications, such as filling up containers, loading trucks with weight capacity constraints, creating file backups in media and technology mapping in Field-programmable gate array semiconductor chip design.
The bin packing problem can also be seen as a special case of the cutting stock problem. When the number of bins is restricted to 1 and each item is characterised by both a volume and a value, the problem of maximising the value of items that can fit in the bin is known as the knapsack problem.
Despite the fact that the bin packing problem has an NP-hard computational complexity, optimal solutions to very large instances of the problem can be produced with sophisticated algorithms. In addition, many heuristics have been developed: for example, the first fit algorithm provides a fast but often non-optimal solution, involving placing each item into the first bin in which it will fit. It requires Θ(n log n) time, where n is the number of elements to be packed. The algorithm can be made much more effective by first sorting the list of elements into decreasing order (sometimes known as the first-fit decreasing algorithm), although this still does not guarantee an optimal solution, and for longer lists may increase the running time of the algorithm. It is known, however, that there always exists at least one ordering of items that allows first-fit to produce an optimal solution.[1]
A variant of bin packing that occurs in practice is when items can share space when packed into a bin. Specifically, a set of items could occupy less space when packed together than the sum of their individual sizes. This variant is known as VM packing[2] since when virtual machines (VMs) are packed in a server, their total memory requirement could decrease due to pages shared by the VMs that need only be stored once. If items can share space in arbitrary ways, the bin packing problem is hard to even approximate. However, if the space sharing fits into a hierarchy, as is the case with memory sharing in virtual machines, the bin packing problem can be efficiently approximated.
Formal statement
Given a bin 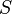 of size
of size  and a list of
and a list of  items with sizes
items with sizes 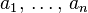 to pack, find an integer number of bins
to pack, find an integer number of bins  and a
and a  -partition
-partition 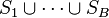 of the set
of the set 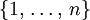 such that
such that 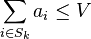 for all
for all 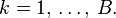 A solution is optimal if it has minimal
A solution is optimal if it has minimal  . The
. The  -value for an optimal solution is denoted OPT below. A possible Integer Linear Programming formulation of the problem is:
-value for an optimal solution is denoted OPT below. A possible Integer Linear Programming formulation of the problem is:
minimize 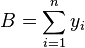 |
||
| subject to | 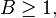 | |
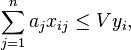 |
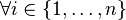 | |
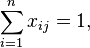 |
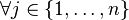 | |
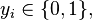 |
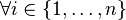 | |
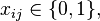 |
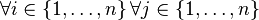 | |
where  if bin
if bin  is used and
is used and 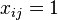 if item
if item 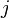 is put into bin
is put into bin  .[3]
.[3]
First-fit algorithm
This is a very straightforward greedy approximation algorithm. The algorithm processes the items in arbitrary order. For each item, it attempts to place the item in the first bin that can accommodate the item. If no bin is found, it opens a new bin and puts the item within the new bin.
It is rather simple to show this algorithm achieves an approximation factor of 2, that is, the number of bins used by this algorithm is no more than twice the optimal number of bins. In other words, it is impossible for 2 bins to be at most half full because such a possibility implies that at some point, exactly one bin was at most half full and a new one was opened to accommodate an item of size at most V/2. But since the first one has at least a space of V / 2, the algorithm will not open a new bin for any item whose size is at most V / 2. Only after the bin fills with more than V / 2 or if an item with a size larger than V / 2 arrives, the algorithm may open a new bin.
Thus if we have B bins, at least B − 1 bins are more than half full. Therefore 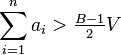 . Because
. Because 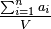 is a lower bound of the optimum value OPT, we get that B − 1 < 2OPT and therefore B ≤ 2OPT.[4] See the analysis below for better approximation results.
is a lower bound of the optimum value OPT, we get that B − 1 < 2OPT and therefore B ≤ 2OPT.[4] See the analysis below for better approximation results.
Alternative proof:
Suppose greedy algorithm returns more than 2 OPT bins. If we take any two successive bins, together they must contain at least V of items ( otherwise only one bin would be sufficient). Since we have at least OPT pairs plus extra bin, we have together more than OPT V items, a contradiction.
Analysis of approximate algorithms
The best fit decreasing and first fit decreasing strategies are among the simplest heuristic algorithms for solving the bin packing problem. They have been shown to use no more than 11/9 OPT + 1 bins (where OPT is the number of bins given by the optimal solution).[5] The simpler of these, the First Fit Decreasing (FFD) strategy, operates by first sorting the items to be inserted in decreasing order by their sizes, and then inserting each item into the first bin in the list with sufficient remaining space. Sometimes, however, one does not have the option to sort the input, for example, when faced with an online bin packing problem. In 2007, it was proven that the bound 11/9 OPT + 6/9 for FFD is tight.[6] MFFD[7] (a variant of FFD) uses no more than 71/60 OPT + 1 bins[8] (i.e. bounded by about 1.18 OPT, compared to about 1.22 OPT for FFD). In 2013, Sgall and Dósa gave a tight upper bound for the first-fit (FF) strategy, showing that it never needs more than 17/10 OPT bins for any input.
It is NP-hard to distinguish whether OPT is 2 or 3, thus for all ε > 0, bin packing is hard to approximate within 3/2 − ε. (If such an approximation exists, one could determine whether n non-negative integers can be partitioned into two sets with the same sum in polynomial time. However, this problem is known to be NP-hard.) Consequently, the bin packing problem does not have a polynomial-time approximation scheme (PTAS) unless P = NP. On the other hand, for any 0 < ε ≤ 1, it is possible to find a solution using at most (1 + ε)OPT + 1 bins in polynomial time. This approximation type is known as asymptotic PTAS.[9][10]
Exact algorithm
Martello and Toth[11] developed an exact algorithm for the 1-D bin-packing problem, called MTP. A faster alternative is the Bin Completion algorithm proposed by Korf in 2002[12] and later improved;[13] this second paper reports the average time to solve one million instances with 80 items on a 440 MHz Sun Ultra 10 workstation was 31 ms.
Software
| Name | License | Brief info |
|---|---|---|
| BPP Spreadsheet Solver | Creative Commons Attribution 4.0 International License | Microsoft Excel and VBA based open source solver. Capable of solving and visualizing two-dimensional bin packing problems with bin and item compatibility constraints. link Video tutorial link |
| OpenOpt | BSD | Free Python language framework that can use either free or commercial MILP and other solvers to solve bin packing problems, possibly constrained, see its BPP page and other available problems |
| OptaPlanner | ASL | Open Source Java constraint solver (optaplanner.org) with several bin packing examples. |
| VPSolver | GPL | Open Source Vector Packing Solver (VPSolver) that can be used to solve to optimality one-dimensional cutting and packing problems as one-dimensional vector packing problems. Vector packing is a generalization of bin packing with multiple constraints. |
See also
- If the number of bins is to be fixed or constrained, and the size of the bins is to be minimised, that is a different problem which is equivalent to the Multiprocessor scheduling problem
- Guillotine problem
- Packing problem
- Partition problem
- Subset sum problem
References
- ↑ Lewis, Rhyd (2009). "A General-Purpose Hill-Climbing Method for Order Independent Minimum Grouping Problems: A Case Study in Graph Colouring and Bin Packing". Computers and Operations Research 36 (7): 2295–2310. doi:10.1016/j.cor.2008.09.004.
- ↑ Sindelar, Sitaraman & Shenoy 2011, pp. 367–378
- ↑ Silvano Martello and Paolo Toth (1990). Knapsack problems (PDF). Chichester, UK: John Wiley and Sons. p. 221. ISBN 0471924202.
- ↑ Vazirani 2003, p. 74.
- ↑ Yue 1991, pp. 321–331.
- ↑ Dósa 2007, pp. 1–11.
- ↑ Garey & Johnson 1985, pp. 65–106.
- ↑ Yue & Zhang 1995, pp. 318–330.
- ↑ Vazirani 2003, pp. 74–76.
- ↑ de la Vega & Lueker 1981, pp. 349–355
- ↑ Martello & Toth 1990, pp. 237–240.
- ↑ Korf 2002
- ↑ R. E. Korf (2003), An improved algorithm for optimal bin packing. Proceedings of the International Joint Conference on Artificial Intelligence, (pp. 1252–1258)
Bibliography
- Korf, Richard E. (2002), A new algorithm for optimal bin packing. (PDF)
- Vazirani, Vijay V. (2003), Approximation Algorithms, Berlin: Springer, ISBN 3-540-65367-8
- Yue, Minyi (October 1991), "A simple proof of the inequality FFD (L) ≤ 11/9 OPT (L) + 1, ∀L for the FFD bin-packing algorithm", Acta Mathematicae Applicatae Sinica 7 (4): 321–331, doi:10.1007/BF02009683, ISSN 0168-9673
|contribution=ignored (help) - Dósa, György (2007), "The Tight Bound of First Fit Decreasing Bin-Packing Algorithm Is FFD(I)≤(11/9)OPT(I)+6/9", in Chen, Bo; Paterson, Mike; Zhang, Guochuan, Combinatorics, Algorithms, Probabilistic and Experimental Methodologies, 4614/2007, Springer Berlin / Heidelberg, pp. 1–11, doi:10.1007/978-3-540-74450-4, ISBN 978-3-540-74449-8, ISSN 0302-9743
- Xia, Binzhou; Tan, Zhiyi (2010), "Tighter bounds of the First Fit algorithm for the bin-packing problem", Discrete Applied Mathematics 158 (15): 1668–1675, doi:10.1016/j.dam.2010.05.026, ISSN 0166-218X
|contribution=ignored (help) - Garey, Michael R.; Johnson, David S. (1985), "A 71/60 theorem for bin packing*1", Journal of Complexity 1: 65–106, doi:10.1016/0885-064X(85)90022-6
|contribution=ignored (help) - Yue, Minyi; Zhang, Lei (July 1995), "A simple proof of the inequality MFFD(L)≤71/60 OPT(L) + 1,L for the MFFD bin-packing algorithm", Acta Mathematicae Applicatae Sinica 11 (3): 318–330, doi:10.1007/BF02011198, ISSN 0168-9673
|contribution=ignored (help) - Fernandez de la Vega, W.; Lueker, G. S. (December 1981), "Bin packing can be solved within 1 + ε in linear time", Combinatorica (Springer Berlin / Heidelberg) 1 (4): 349–355, doi:10.1007/BF02579456, ISSN 0209-9683
|contribution=ignored (help) - Lewis, R. (2009), "A General-Purpose Hill-Climbing Method for Order Independent Minimum Grouping Problems: A Case Study in Graph Colouring and Bin Packing", Computers and Operations Research 36 (7): 2295–2310, doi:10.1016/j.cor.2008.09.004
- Silvano Martello and Paolo Toth (1990), Knapsack Problems Algorithms and Computer Implementations.
- Michael R. Garey and David S. Johnson (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman. ISBN 0-7167-1045-5. A4.1: SR1, p. 226.
- David S. Johnson, Alan J. Demers, Jeffrey D. Ullman, M. R. Garey, Ronald L. Graham. Worst-Case Performance Bounds for Simple One-Dimensional Packing Algorithms. SICOMP, Volume 3, Issue 4. 1974.
- Lodi A., Martello S., Monaci, M., Vigo, D. (2010) Two-Dimensional Bin Packing Problems. In V.Th. Paschos (Ed.), “Paradigms of Combinatorial Optimization”, Wiley/ISTE, p. 107-129
- Dósa G., Sgall J. (2013) First Fit bin packing: A tight analysis. To appear in STACS 2013.
- Sindelar, Michael; Sitaraman, Ramesh; Shenoy, Prashant (2011), "Sharing-Aware Algorithms for Virtual Machine Colocation", Proceedings of 23rd ACM Symposium on Parallelism in Algorithms and Architectures (SPAA), San Jose, CA, June 2011: 367–378
External links
- PHP Class to pack files without exceeding a given size limit
- An implementation of several bin packing heuristics in Haskell, including FFD and MFFD.
- Cutting And Packing Algorithms Research Framework, including a number of bin packing algorithms and test data.
- A simple on-line bin-packing algorithm
- Optimizing Three-Dimensional Bin Packing
- Fpart : open-source command-line tool to pack files (C, BSD-licensed)
- Bin Packing and Cutting Stock Solver Algorithm
| ||||||||||||||||||